Tidy Time Series Analysis, Part 4: Lags and Autocorrelation
Written by Matt Dancho
In the fourth part in a series on Tidy Time Series Analysis, we’ll investigate lags and autocorrelation, which are useful in understanding seasonality and form the basis for autoregressive forecast models such as AR, ARMA, ARIMA, SARIMA (basically any forecast model with “AR” in the acronym). We’ll use the tidyquant package along with our tidyverse downloads data obtained from cranlogs. The focus of this post is using lag.xts(), a function capable of returning multiple lags from a xts object, to investigate autocorrelation in lags among the daily tidyverse package downloads. When using lag.xts() with tq_mutate() we can scale to multiple groups (different tidyverse packages in our case). If you like what you read, please follow us on social media to stay up on the latest Business Science news, events and information! As always, we are interested in both expanding our network of data scientists and seeking new clients interested in applying data science to business and finance. If interested, contact us.
If you haven’t checked out the previous tidy time series posts, you may want to review them to get up to speed.
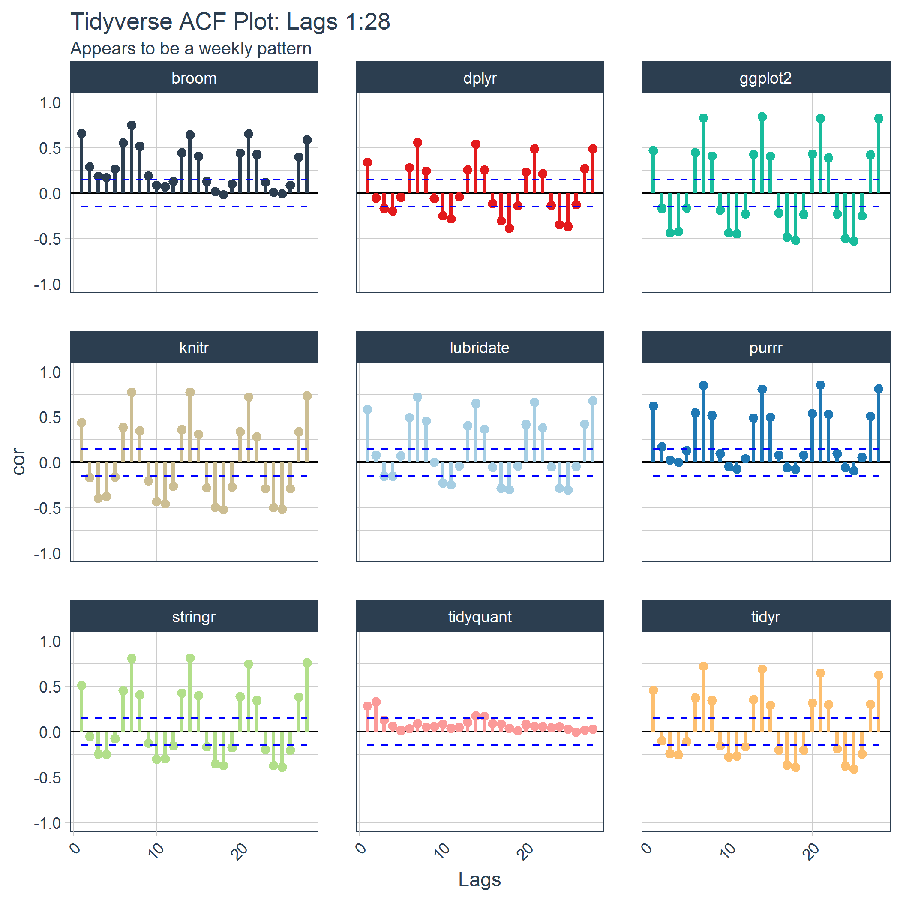
Here’s an example of the autocorrelation plot we investigate as part of this post:

Libraries Needed
We’ll need to load several libraries today.
library(tidyquant) # Loads tidyverse, tidyquant, financial pkgs, xts/zoo
library(cranlogs) # For inspecting package downloads over time
library(timetk) # For consistent time series coercion functions
library(stringr) # Working with strings
library(forcats) # Working with factors/categorical data
CRAN tidyverse Downloads
We’ll be using the same “tidyverse” dataset as the last several posts. The script below gets the package downloads for the first half of 2017.
# tidyverse packages (see my laptop stickers from first post) ;)
pkgs <- c(
"tidyr", "lubridate", "dplyr",
"broom", "tidyquant", "ggplot2", "purrr",
"stringr", "knitr"
)
# Get the downloads for the individual packages
tidyverse_downloads <- cran_downloads(
packages = pkgs,
from = "2017-01-01",
to = "2017-06-30") %>%
tibble::as_tibble() %>%
group_by(package)
tidyverse_downloads
## # A tibble: 1,629 x 3
## # Groups: package [9]
## date count package
## * <date> <dbl> <chr>
## 1 2017-01-01 873 tidyr
## 2 2017-01-02 1840 tidyr
## 3 2017-01-03 2495 tidyr
## 4 2017-01-04 2906 tidyr
## 5 2017-01-05 2847 tidyr
## 6 2017-01-06 2756 tidyr
## 7 2017-01-07 1439 tidyr
## 8 2017-01-08 1556 tidyr
## 9 2017-01-09 3678 tidyr
## 10 2017-01-10 7086 tidyr
## # ... with 1,619 more rows
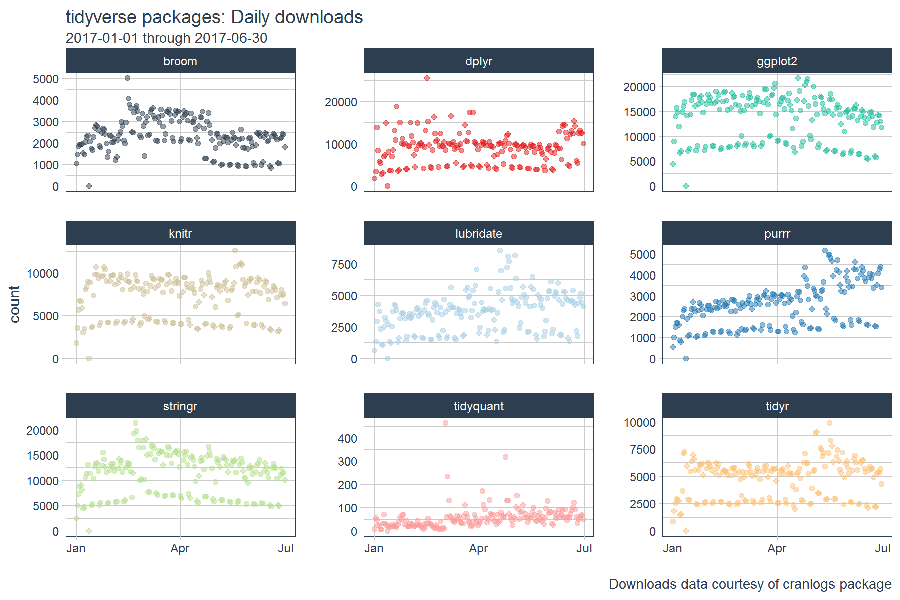
We can visualize daily downloads, but detecting the trend is quite difficult due to noise in the data.
# Visualize the package downloads
tidyverse_downloads %>%
ggplot(aes(x = date, y = count, color = package)) +
# Data
geom_point(alpha = 0.5) +
facet_wrap(~ package, ncol = 3, scale = "free_y") +
# Aesthetics
labs(title = "tidyverse packages: Daily downloads", x = "",
subtitle = "2017-01-01 through 2017-06-30",
caption = "Downloads data courtesy of cranlogs package") +
scale_color_tq() +
theme_tq() +
theme(legend.position="none")
Lags (Lag Operator)
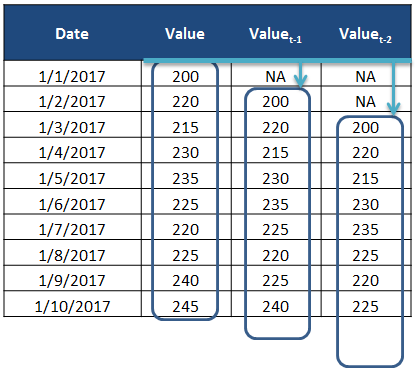
The lag operator (also known as backshift operator) is a function that shifts (offsets) a time series such that the “lagged” values are aligned with the actual time series. The lags can be shifted any number of units, which simply controls the length of the backshift. The picture below illustrates the lag operation for lags 1 and 2.
Lags are very useful in time series analysis because of a phenomenon called autocorrelation, which is a tendency for the values within a time series to be correlated with previous copies of itself. One benefit to autocorrelation is that we can identify patterns within the time series, which helps in determining seasonality, the tendency for patterns to repeat at periodic frequencies. Understanding how to calculate lags and analyze autocorrelation will be the focus of this post.
Finally, lags and autocorrelation are central to numerous forecasting models that incorporate autoregression, regressing a time series using previous values of itself. Autoregression is the basis for one of the most widely used forecasting techniques, the autoregressive integrated moving average model or ARIMA for short. Possibly the most widely used tool for forecasting, the forecast package by Rob Hyndman, implements ARIMA (and a number of other forecast modeling techniques). We’ll save autoregression and ARIMA for another day as the subject is truly fascinating and deserves its own focus.
Background on Functions Used
The xts, zoo, and TTR packages have some great functions that enable working with time series. The tidyquant package enables a “tidy” implementation of these functions. You can see which functions are integrated into tidyquant package using tq_mutate_fun_options(). We use glimpse() to shorten the output.
# tidyquant Integrated functions
tq_mutate_fun_options() %>%
glimpse()
## List of 5
## $ zoo : chr [1:14] "rollapply" "rollapplyr" "rollmax" "rollmax.default" ...
## $ xts : chr [1:27] "apply.daily" "apply.monthly" "apply.quarterly" "apply.weekly" ...
## $ quantmod : chr [1:25] "allReturns" "annualReturn" "ClCl" "dailyReturn" ...
## $ TTR : chr [1:62] "adjRatios" "ADX" "ALMA" "aroon" ...
## $ PerformanceAnalytics: chr [1:7] "Return.annualized" "Return.annualized.excess" "Return.clean" "Return.cumulative" ...
lag.xts()
Today, we’ll take a look at the lag.xts() function from the xts package, which is a really great function for getting multiple lags. Before we dive into an analysis, let’s see how the function works. Say we have a time series of ten values beginning in 2017.
set.seed(1)
my_time_series_tbl <- tibble(
date = seq.Date(ymd("2017-01-01"), length.out = 10, by = "day"),
value = 1:10 + rnorm(10)
)
my_time_series_tbl
## # A tibble: 10 x 2
## date value
## <date> <dbl>
## 1 2017-01-01 0.3735462
## 2 2017-01-02 2.1836433
## 3 2017-01-03 2.1643714
## 4 2017-01-04 5.5952808
## 5 2017-01-05 5.3295078
## 6 2017-01-06 5.1795316
## 7 2017-01-07 7.4874291
## 8 2017-01-08 8.7383247
## 9 2017-01-09 9.5757814
## 10 2017-01-10 9.6946116
The lag.xts() function generates a sequence of lags (t-1, t-2, t-3, …, t-k) using the argument k. However, it only works on xts objects (or other matrix, vector-based objects). In other words, it fails on our “tidy” tibble. We get an “unsupported type” error.
# Bummer, man!
my_time_series_tbl %>%
lag.xts(k = 1:5)
## <simpleError in FUN(X[[i]], ...): unsupported type>
Now, watch what happens when converted to an xts object. We’ll use tk_xts() from the timetk package to coerce from a time-based tibble (tibble with a date or time component) to and xts object.
The timetk package is a toolkit for working with time series. It has functions that simplify and make consistent the process of coercion (converting to and from different time series classes). In addition, it has functions to aid the process of time series machine learning and data mining. Visit the docs to learn more.
# Success! Got our lags 1 through 5. One problem: no original values
my_time_series_tbl %>%
tk_xts(silent = TRUE) %>%
lag.xts(k = 1:5)
## value value.1 value.2 value.3 value.4
## 2017-01-01 NA NA NA NA NA
## 2017-01-02 0.3735462 NA NA NA NA
## 2017-01-03 2.1836433 0.3735462 NA NA NA
## 2017-01-04 2.1643714 2.1836433 0.3735462 NA NA
## 2017-01-05 5.5952808 2.1643714 2.1836433 0.3735462 NA
## 2017-01-06 5.3295078 5.5952808 2.1643714 2.1836433 0.3735462
## 2017-01-07 5.1795316 5.3295078 5.5952808 2.1643714 2.1836433
## 2017-01-08 7.4874291 5.1795316 5.3295078 5.5952808 2.1643714
## 2017-01-09 8.7383247 7.4874291 5.1795316 5.3295078 5.5952808
## 2017-01-10 9.5757814 8.7383247 7.4874291 5.1795316 5.3295078
We get our lags! However, we still have one problem: We need our original values so we can analyze the counts against the lags. If we want to get the original values too, we can do something like this.
# Convert to xts
my_time_series_xts <- my_time_series_tbl %>%
tk_xts(silent = TRUE)
# Get original values and lags in xts
my_lagged_time_series_xts <-
merge.xts(my_time_series_xts, lag.xts(my_time_series_xts, k = 1:5))
# Convert back to tbl
my_lagged_time_series_xts %>%
tk_tbl()
## # A tibble: 10 x 7
## index value value.5 value.1 value.2 value.3
## <date> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 2017-01-01 0.3735462 NA NA NA NA
## 2 2017-01-02 2.1836433 0.3735462 NA NA NA
## 3 2017-01-03 2.1643714 2.1836433 0.3735462 NA NA
## 4 2017-01-04 5.5952808 2.1643714 2.1836433 0.3735462 NA
## 5 2017-01-05 5.3295078 5.5952808 2.1643714 2.1836433 0.3735462
## 6 2017-01-06 5.1795316 5.3295078 5.5952808 2.1643714 2.1836433
## 7 2017-01-07 7.4874291 5.1795316 5.3295078 5.5952808 2.1643714
## 8 2017-01-08 8.7383247 7.4874291 5.1795316 5.3295078 5.5952808
## 9 2017-01-09 9.5757814 8.7383247 7.4874291 5.1795316 5.3295078
## 10 2017-01-10 9.6946116 9.5757814 8.7383247 7.4874291 5.1795316
## # ... with 1 more variables: value.4 <dbl>
That’s a lot of work for a simple operation. Fortunately we have tq_mutate() to the rescue!
tq_mutate()
The tq_mutate() function from tidyquant enables “tidy” application of the xts-based functions. The tq_mutate() function works similarly to mutate() from dplyr in the sense that it adds columns to the data frame.
The tidyquant package enables a “tidy” implementation of the xts-based functions from packages such as xts, zoo, quantmod, TTR and PerformanceAnalytics. Visit the docs to learn more.
Here’s a quick example. We use the select = value to send the “value” column to the mutation function. In this case our mutate_fun = lag.xts. We supply k = 5 as an additional argument.
# This is nice, we didn't need to coerce to xts and it merged for us
my_time_series_tbl %>%
tq_mutate(
select = value,
mutate_fun = lag.xts,
k = 1:5
)
## # A tibble: 10 x 7
## date value value.1 value.2 value.3 value.4
## <date> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 2017-01-01 0.3735462 NA NA NA NA
## 2 2017-01-02 2.1836433 0.3735462 NA NA NA
## 3 2017-01-03 2.1643714 2.1836433 0.3735462 NA NA
## 4 2017-01-04 5.5952808 2.1643714 2.1836433 0.3735462 NA
## 5 2017-01-05 5.3295078 5.5952808 2.1643714 2.1836433 0.3735462
## 6 2017-01-06 5.1795316 5.3295078 5.5952808 2.1643714 2.1836433
## 7 2017-01-07 7.4874291 5.1795316 5.3295078 5.5952808 2.1643714
## 8 2017-01-08 8.7383247 7.4874291 5.1795316 5.3295078 5.5952808
## 9 2017-01-09 9.5757814 8.7383247 7.4874291 5.1795316 5.3295078
## 10 2017-01-10 9.6946116 9.5757814 8.7383247 7.4874291 5.1795316
## # ... with 1 more variables: value.5 <dbl>
That’s much easier. We get the value column returned in addition to the lags, which is the benefit of using tq_mutate(). If you use tq_transmute() instead, the result would be the lags only, which is what lag.xts() returns.
Analyzing tidyverse Downloads: Lag and Autocorrelation Analysis
Now that we understand a little more about lags and the lag.xts() and tq_mutate() functions, let’s put this information to use with a lag and autocorrelation analysis of the tidyverse package downloads. We’ll analyze all tidyverse packages together, showing off the scalability of tq_mutate().
Scaling the Lag and Autocorrelation Calculation
First, let’s get lags 1 through 28 (4 weeks of lags). The process is quite simple: we take the tidyverse_downloads data frame, which is grouped by package, and apply tq_mutate() using the lag.xts function. We can provide column names for the new columns by prefixing “lag_” to the lag numbers, k, which the sequence from 1 to 28. The output is all of the lags for each package.
# Use tq_mutate() to get lags 1:28 using lag.xts()
k <- 1:28
col_names <- paste0("lag_", k)
tidyverse_lags <- tidyverse_downloads %>%
tq_mutate(
select = count,
mutate_fun = lag.xts,
k = 1:28,
col_rename = col_names
)
tidyverse_lags
## # A tibble: 1,629 x 31
## # Groups: package [9]
## package date count lag_1 lag_2 lag_3 lag_4 lag_5 lag_6 lag_7
## <chr> <date> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 tidyr 2017-01-01 873 NA NA NA NA NA NA NA
## 2 tidyr 2017-01-02 1840 873 NA NA NA NA NA NA
## 3 tidyr 2017-01-03 2495 1840 873 NA NA NA NA NA
## 4 tidyr 2017-01-04 2906 2495 1840 873 NA NA NA NA
## 5 tidyr 2017-01-05 2847 2906 2495 1840 873 NA NA NA
## 6 tidyr 2017-01-06 2756 2847 2906 2495 1840 873 NA NA
## 7 tidyr 2017-01-07 1439 2756 2847 2906 2495 1840 873 NA
## 8 tidyr 2017-01-08 1556 1439 2756 2847 2906 2495 1840 873
## 9 tidyr 2017-01-09 3678 1556 1439 2756 2847 2906 2495 1840
## 10 tidyr 2017-01-10 7086 3678 1556 1439 2756 2847 2906 2495
## # ... with 1,619 more rows, and 21 more variables: lag_8 <dbl>,
## # lag_9 <dbl>, lag_10 <dbl>, lag_11 <dbl>, lag_12 <dbl>,
## # lag_13 <dbl>, lag_14 <dbl>, lag_15 <dbl>, lag_16 <dbl>,
## # lag_17 <dbl>, lag_18 <dbl>, lag_19 <dbl>, lag_20 <dbl>,
## # lag_21 <dbl>, lag_22 <dbl>, lag_23 <dbl>, lag_24 <dbl>,
## # lag_25 <dbl>, lag_26 <dbl>, lag_27 <dbl>, lag_28 <dbl>
Next, we need to correlate each of the lags to the “count” column. This involves a few steps that can be strung together in a dplyr pipe (%>%):
-
The goal is to get count and each lag side-by-side so we can do a correlation. To do this we use gather() to pivot each of the lagged columns into a “tidy” (long format) data frame, and we exclude “package”, “date”, and “count” columns from the pivot.
-
Next, we convert the new “lag” column from a character string (e.g. “lag_1”) to numeric (e.g. 1) using mutate(), which will make ordering the lags much easier.
-
Next, we group the long data frame by package and lag. This allows us to calculate using subsets of package and lag.
-
Finally, we apply the correlation to each group of lags. The summarize() function can be used to implement cor(), which takes x = count and y = lag_value. Make sure to pass use = "pairwise.complete.obs", which is almost always desired. Additionally, the 95% upper and lower cutoff can be approximated by:
$$cutoff = \pm \frac{2}{N^{0.5}}$$
Where:
- N = number of observations.
Putting it all together:
# Calculate the autocorrelations and 95% cutoffs
tidyverse_count_autocorrelations <- tidyverse_lags %>%
gather(key = "lag", value = "lag_value", -c(package, date, count)) %>%
mutate(lag = str_sub(lag, start = 5) %>% as.numeric) %>%
group_by(package, lag) %>%
summarize(
cor = cor(x = count, y = lag_value, use = "pairwise.complete.obs"),
cutoff_upper = 2/(n())^0.5,
cutoff_lower = -2/(n())^0.5
)
tidyverse_count_autocorrelations
## # A tibble: 252 x 5
## # Groups: package [?]
## package lag cor cutoff_upper cutoff_lower
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 broom 1 0.65709555 0.1486588 -0.1486588
## 2 broom 2 0.29065629 0.1486588 -0.1486588
## 3 broom 3 0.18617353 0.1486588 -0.1486588
## 4 broom 4 0.17266972 0.1486588 -0.1486588
## 5 broom 5 0.26686998 0.1486588 -0.1486588
## 6 broom 6 0.55222426 0.1486588 -0.1486588
## 7 broom 7 0.74755610 0.1486588 -0.1486588
## 8 broom 8 0.51461062 0.1486588 -0.1486588
## 9 broom 9 0.19069218 0.1486588 -0.1486588
## 10 broom 10 0.08473241 0.1486588 -0.1486588
## # ... with 242 more rows
Visualizing Autocorrelation: ACF Plot
Now that we have the correlations calculated by package and lag number in a nice “tidy” format, we can visualize the autocorrelations with ggplot to check for patterns. The plot shown below is known as an ACF plot, which is simply the autocorrelations at various lags. Initial examination of the ACF plots indicate a weekly frequency.
# Visualize the autocorrelations
tidyverse_count_autocorrelations %>%
ggplot(aes(x = lag, y = cor, color = package, group = package)) +
# Add horizontal line a y=0
geom_hline(yintercept = 0) +
# Plot autocorrelations
geom_point(size = 2) +
geom_segment(aes(xend = lag, yend = 0), size = 1) +
# Add cutoffs
geom_line(aes(y = cutoff_upper), color = "blue", linetype = 2) +
geom_line(aes(y = cutoff_lower), color = "blue", linetype = 2) +
# Add facets
facet_wrap(~ package, ncol = 3) +
# Aesthetics
expand_limits(y = c(-1, 1)) +
scale_color_tq() +
theme_tq() +
labs(
title = paste0("Tidyverse ACF Plot: Lags ", rlang::expr_text(k)),
subtitle = "Appears to be a weekly pattern",
x = "Lags"
) +
theme(
legend.position = "none",
axis.text.x = element_text(angle = 45, hjust = 1)
)
Which Lags Consistently Stand Out?
We see that there appears to be a weekly pattern, but we want to be sure. We can verify the weekly pattern assessment by reviewing the absolute value of the correlations independent of package. We take the absolute autocorrelation because we use the magnitude as a proxy for how much explanatory value the lag provides. We’ll use dplyr functions to manipulate the data for visualization:
-
We drop the package group constraint using ungroup().
-
We calculate the absolute correlation using mutate(). We also convert the lag to a factor, which helps with reordering the plot later.
-
We select() only the “lag” and “cor_abs” columns.
-
We group by “lag” to lump all of the lags together. This enables us to determine the trend independent of package.
# Get the absolute autocorrelations
tidyverse_absolute_autocorrelations <- tidyverse_count_autocorrelations %>%
ungroup() %>%
mutate(
lag = as_factor(as.character(lag)),
cor_abs = abs(cor)
) %>%
select(lag, cor_abs) %>%
group_by(lag)
tidyverse_absolute_autocorrelations
## # A tibble: 252 x 2
## # Groups: lag [28]
## lag cor_abs
## <fctr> <dbl>
## 1 1 0.65709555
## 2 2 0.29065629
## 3 3 0.18617353
## 4 4 0.17266972
## 5 5 0.26686998
## 6 6 0.55222426
## 7 7 0.74755610
## 8 8 0.51461062
## 9 9 0.19069218
## 10 10 0.08473241
## # ... with 242 more rows
We can now visualize the absolute correlations using a box plot that lumps each of the lags together. We can add a line to indicate the presence of outliers at values above \(1.5IQR\). If the values are consistently above this limit, the lag can be considered an outlier. Note that we use the fct_reorder() function from forcats to organize the boxplot in order of decending magnitude.
# Visualize boxplot of absolute autocorrelations
break_point <- 1.5*IQR(tidyverse_absolute_autocorrelations$cor_abs) %>% signif(3)
tidyverse_absolute_autocorrelations %>%
ggplot(aes(x = fct_reorder(lag, cor_abs, .desc = TRUE) , y = cor_abs)) +
# Add boxplot
geom_boxplot(color = palette_light()[[1]]) +
# Add horizontal line at outlier break point
geom_hline(yintercept = break_point, color = "red") +
annotate("text", label = paste0("Outlier Break Point = ", break_point),
x = 24.5, y = break_point + .03, color = "red") +
# Aesthetics
expand_limits(y = c(0, 1)) +
theme_tq() +
labs(
title = paste0("Absolute Autocorrelations: Lags ", rlang::expr_text(k)),
subtitle = "Weekly pattern is consistently above outlier break point",
x = "Lags"
) +
theme(
legend.position = "none",
axis.text.x = element_text(angle = 45, hjust = 1)
)
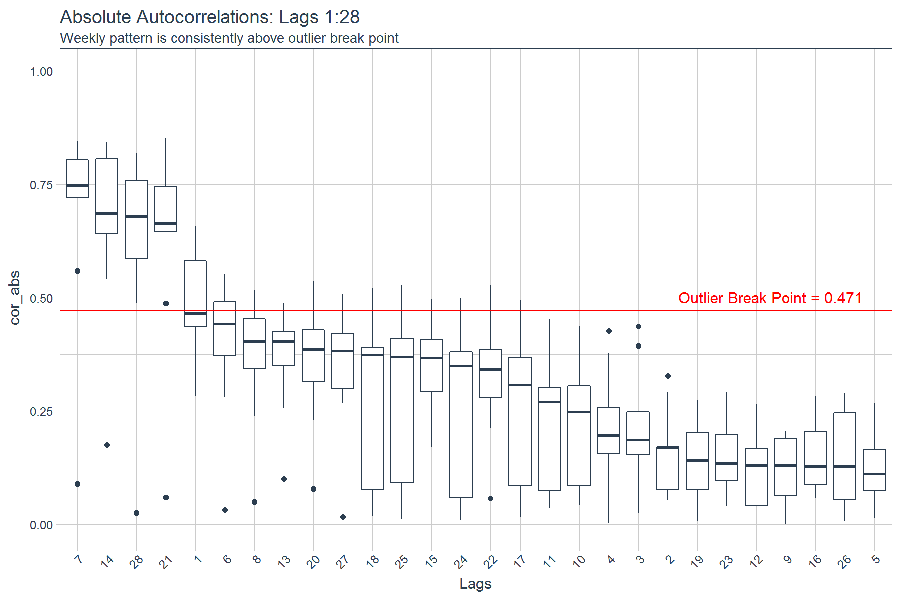
Lags in multiples of seven have the highest autocorrelation and are consistently above the outlier break point indicating the presence of a strong weekly pattern. The autocorrelation with the seven-day lag is the highest, with a median of approximately 0.75. Lags 14, 21, and 28 are also outliers with median autocorrelations in excess of our outlier break point of 0.471.
Note that the median of Lag 1 is essentially at the break point indicating that half of the packages have a presence of “abnormal” autocorrelation. However, this is not part of a seasonal pattern since a periodic frequency is not present.
Conclusions
Lag and autocorrelation analysis is a good way to detect seasonality. We used the autocorrelation of the lagged values to detect “abnormal” seasonal patterns. In this case, the tidyverse packages exhibit a strong weekly pattern. We saw how the tq_mutate() function was used to apply lag.xts() to the daily download counts to efficiently get lags 1 through 28. Once the lags were retrieved, we used other dplyr functions such as gather() to pivot the data and summarize() to calculate the autocorrelations. Finally, we saw the power of visual analysis of the autocorrelations. We created an ACF plot that showed a visual trend. Then we used a boxplot to detect which lags had consistent outliers. Ultimately a weekly pattern was confirmed.
Business Science University
Enjoy data science for business? We do too. This is why we created Business Science University where we teach you how to do Data Science For Busines (#DS4B) just like us!
Our first DS4B course (HR 201) is now available!
Who is this course for?
Anyone that is interested in applying data science in a business context (we call this DS4B). All you need is basic R, dplyr, and ggplot2 experience. If you understood this article, you are qualified.
What do you get it out of it?
You learn everything you need to know about how to apply data science in a business context:
-
Using ROI-driven data science taught from consulting experience!
-
Solve high-impact problems (e.g. $15M Employee Attrition Problem)
-
Use advanced, bleeding-edge machine learning algorithms (e.g. H2O, LIME)
-
Apply systematic data science frameworks (e.g. Business Science Problem Framework)
“If you’ve been looking for a program like this, I’m happy to say it’s finally here! This is what I needed when I first began data science years ago. It’s why I created Business Science University.”
Matt Dancho, Founder of Business Science