Time Series Analysis: KERAS LSTM Deep Learning - Part 1
Written by Matt Dancho
Time series prediction (forecasting) has experienced dramatic improvements in predictive accuracy as a result of the data science machine learning and deep learning evolution. As these ML/DL tools have evolved, businesses and financial institutions are now able to forecast better by applying these new technologies to solve old problems. In this article, we showcase the use of a special type of Deep Learning model called an LSTM (Long Short-Term Memory), which is useful for problems involving sequences with autocorrelation. We analyze a famous historical data set called “sunspots” (a sunspot is a solar phenomenon wherein a dark spot forms on the surface of the sun). We’ll show you how you can use an LSTM model to predict sunspots ten years into the future with an LSTM model.
Articles In This Series
Tutorial Overview
This code tutorial goes along with a presentation on Time Series Deep Learning given to SP Global on Thursday, April 19, 2018. The slide deck that complements this article is available for download.
This is an advanced tutorial implementing deep learning for time series and several other complex machine learning topics such as backtesting cross validation. For those seeking an introduction to Keras in R, please check out Customer Analytics: Using Deep Learning With Keras To Predict Customer Churn.
In this tutorial, you will learn how to:
- Develop a Stateful LSTM Model with the
keras package, which connects to the R TensorFlow backend.
- Apply a Keras Stateful LSTM Model to a famous time series, Sunspots.
- Perform Time Series Cross Validation using Backtesting with the
rsample package rolling forecast origin resampling.
- Visualize Backtest Sampling Plans and Prediction Results with
ggplot2 and cowplot.
- Evaluate whether or not a time series may be a good candidate for an LSTM model by reviewing the Autocorrelation Function (ACF) plot.
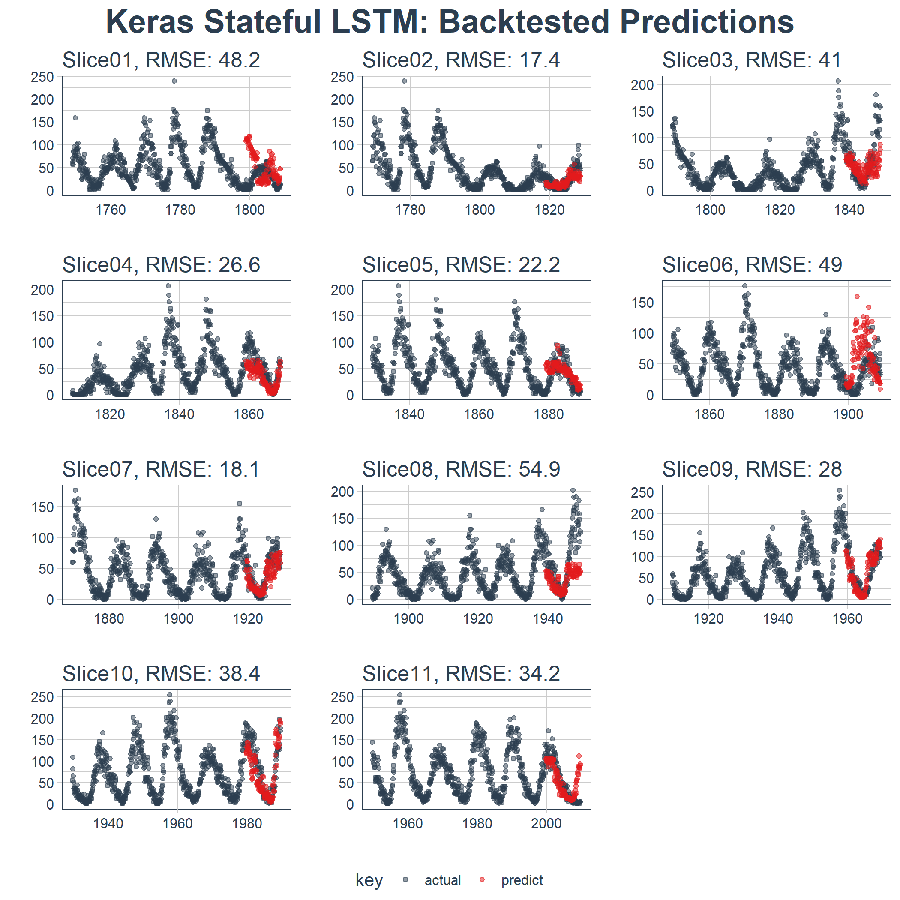
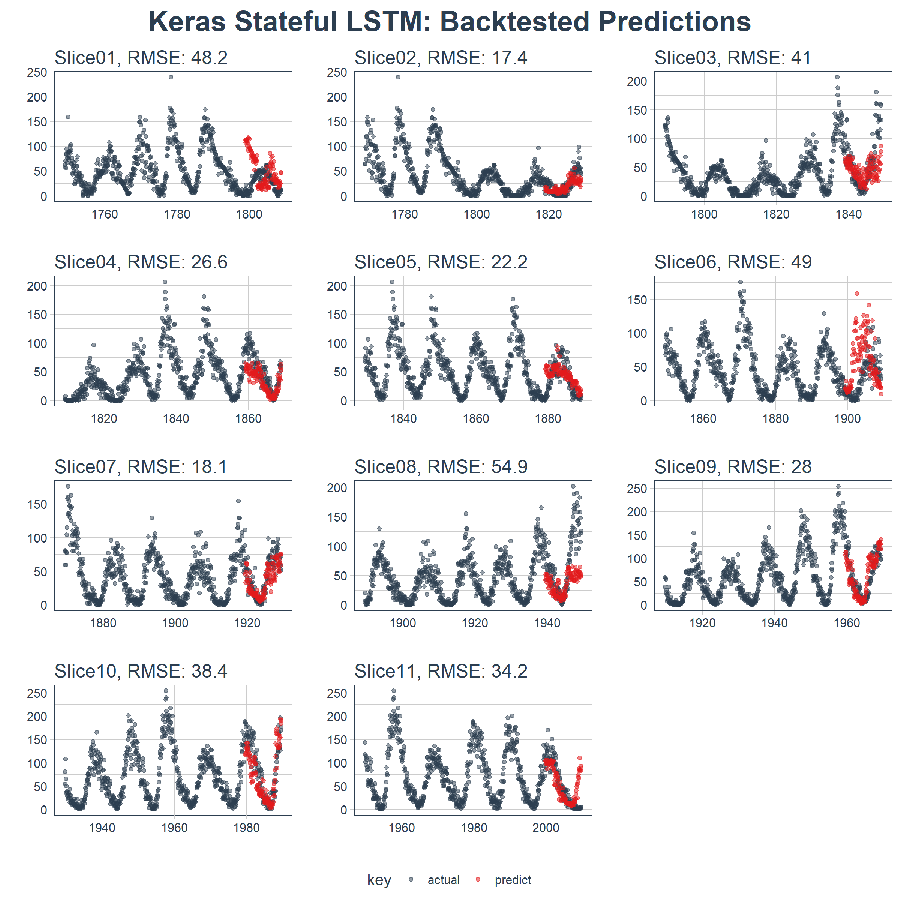
The end result is a high performance deep learning algorithm that does an excellent job at predicting ten years of sunspots! Here’s the plot of the Backtested Keras Stateful LSTM Model.

Applications in Business
Time series prediction (forecasting) has a dramatic effect on the top and bottom line. In business, we could be interested in predicting which day of the month, quarter, or year that large expenditures are going to occur or we could be interested in understanding how the consumer price index (CPI) will change over the course of the next six months. These are common questions that impact organizations both on a microeconomic and macroeconomic level. While the data set used in this tutorial is not a “business” data set, it shows the power of the tool-problem fit, meaning that using the right tool for the job can offer tremendous improvements in accuracy. The net result is increased prediction accuracy ultimately leads to quantifiable improvements to the top and bottom line.
Long Short-Term Memory (LSTM) Models
A Long Short-Term Memory (LSTM) model is a powerful type of recurrent neural network (RNN). The blog article, “Understanding LSTM Networks”, does an excellent job at explaining the underlying complexity in an easy to understand way. Here’s an image depicting the LSTM internal cell architecture that enables it to persist for long term states (in addition to short term), which traditional RNN’s have difficulty with:
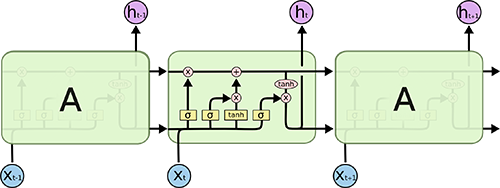
Source: Understanding LSTM Networks
LSTMs are quite useful in time series prediction tasks involving autocorrelation, the presence of correlation between the time series and lagged versions of itself, because of their ability to maintain state and recognize patterns over the length of the time series. The recurrent architecture enables the states to persist, or communicate between updates of the weights as each epoch progresses. Further, the LSTM cell architecture enhances the RNN by enabling long term persistence in addition to short term, which is fascinating!
In Keras, LSTM’s can be operated in a “stateful” mode, which according to the Keras documentation:
The last state for each sample at index i in a batch will be used as initial state for the sample of index i in the following batch
In normal (or “stateless”) mode, Keras shuffles the samples, and the dependencies between the time series and the lagged version of itself are lost. However, when run in “stateful” mode, we can often get high accuracy results by leveraging the autocorrelations present in the time series.
We’ll explain more as we go through this tutorial. For now, just understand that LSTM’s can be really useful for time series problems involving autocorrelation and Keras has the capability to create stateful LSTMs that are perfect for time series modeling.
Sunspots Data Set
Sunspots is a famous data set that ships with R (refer to the datasets library). The dataset tracks sunspots, which are the occurrence of a dark spot on the sun. Here’s an image from NASA showing the solar phenomenon. Pretty cool!

Source: NASA
The dataset we use in this tutorial is called sunspots.month, and it contains 265 years (from 1749 through 2013) of monthly data on number of sunspots per month.
Implementing An LSTM To Predict Sunspots
Time to get to business. Let’s predict sunspots. Here’s our objective:
Objective:
Use an LSTM model to generate a forecast of sunspots that spans 10-years into the future.
1.0 Libraries
Here are the libraries needed for this tutorial. All are available on CRAN. You can install with install.packages() if you do not have them installed already. NOTE: Before proceeding with this code tutorial, make sure to update all packages as previous versions of these packages may not be compatible with the code used. One issue we are aware of is upgrading to lubridate version 1.7.4.
# Core Tidyverse
library(tidyverse)
library(glue)
library(forcats)
# Time Series
library(timetk)
library(tidyquant)
library(tibbletime)
# Visualization
library(cowplot)
# Preprocessing
library(recipes)
# Sampling / Accuracy
library(rsample)
library(yardstick)
# Modeling
library(keras)
If you have not previously run Keras in R, you will need to install Keras using the install_keras() function.
# Install Keras if you have not installed before
install_keras()
2.0 Data
The dataset, sunspot.month, is available for all of us (it ships with base R). It’s a ts class (not tidy), so we’ll convert to a tidy data set using the tk_tbl() function from timetk. We use this instead of as.tibble() from tibble to automatically preserve the time series index as a zoo yearmon index. Last, we’ll convert the zoo index to date using lubridate::as_date() (loaded with tidyquant) and then change to a tbl_time object to make time series operations easier.
sun_spots <- datasets::sunspot.month %>%
tk_tbl() %>%
mutate(index = as_date(index)) %>%
as_tbl_time(index = index)
sun_spots
## # A time tibble: 3,177 x 2
## # Index: index
## index value
## <date> <dbl>
## 1 1749-01-01 58.0
## 2 1749-02-01 62.6
## 3 1749-03-01 70.0
## 4 1749-04-01 55.7
## 5 1749-05-01 85.0
## 6 1749-06-01 83.5
## 7 1749-07-01 94.8
## 8 1749-08-01 66.3
## 9 1749-09-01 75.9
## 10 1749-10-01 75.5
## # ... with 3,167 more rows
3.0 Exploratory Data Analysis
The time series is long (265 years!). We can visualize the time series both full (265 years) and zoomed in on the first 50 years to get a feel for the series.
3.1 Visualizing Sunspot Data With Cowplot
We’ll make to ggplots and combine them using cowplot::plot_grid(). Note that for the zoomed in plot, we make use of tibbletime::time_filter(), which is an easy way to perform time-based filtering.
p1 <- sun_spots %>%
ggplot(aes(index, value)) +
geom_point(color = palette_light()[[1]], alpha = 0.5) +
theme_tq() +
labs(
title = "From 1749 to 2013 (Full Data Set)"
)
p2 <- sun_spots %>%
filter_time("start" ~ "1800") %>%
ggplot(aes(index, value)) +
geom_line(color = palette_light()[[1]], alpha = 0.5) +
geom_point(color = palette_light()[[1]]) +
geom_smooth(method = "loess", span = 0.2, se = FALSE) +
theme_tq() +
labs(
title = "1749 to 1800 (Zoomed In To Show Cycle)",
caption = "datasets::sunspot.month"
)
p_title <- ggdraw() +
draw_label("Sunspots", size = 18, fontface = "bold", colour = palette_light()[[1]])
plot_grid(p_title, p1, p2, ncol = 1, rel_heights = c(0.1, 1, 1))
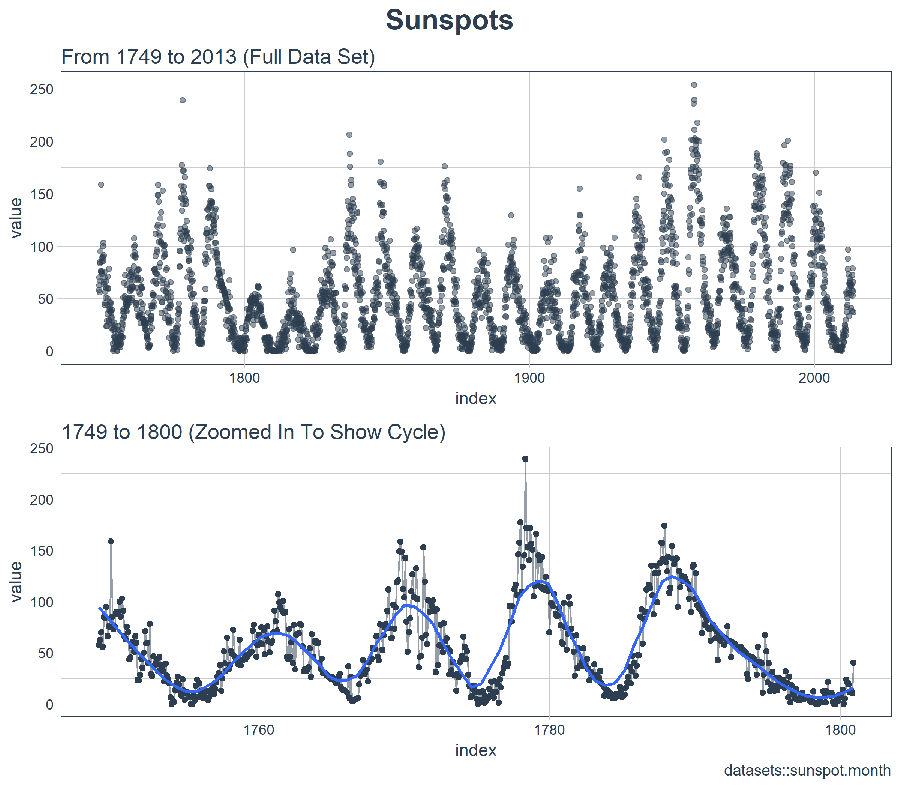
At first glance, it looks like this series should be easy to predict. However, we can see that the cycle (10-year frequency) and amplitude (count of sunspots) seems to change at least between years 1780 and 1800. This creates some challenges.
3.2 Evaluating The ACF
The next thing we can do is determine whether or not an LSTM model may be a good approach. The LSTM will leverage autocorrelation to generate sequence predictions. Our goal is to produce a 10-year forecast using batch forecasting (a technique for creating a single forecast batch across the forecast region, which is in contrast to a single-prediction that is iteratively performed one or several steps into the future). The batch prediction will only work if the autocorrelation used is beyond ten years. Let’s inspect.
First, we need to review the Autocorrelation Function (ACF), which is the correlation between the time series of interest in lagged versions of itself. The acf() function from the stats library returns the ACF values for each lag as a plot. However, we’d like to get the ACF values as data so we can investigate the underlying data. To do so, we’ll create a custom function, tidy_acf(), to return the ACF values in a tidy tibble.
tidy_acf <- function(data, value, lags = 0:20) {
value_expr <- enquo(value)
acf_values <- data %>%
pull(value) %>%
acf(lag.max = tail(lags, 1), plot = FALSE) %>%
.$acf %>%
.[,,1]
ret <- tibble(acf = acf_values) %>%
rowid_to_column(var = "lag") %>%
mutate(lag = lag - 1) %>%
filter(lag %in% lags)
return(ret)
}
Next, let’s test the function out to make sure it works as intended. The function takes our tidy time series, extracts the value column, and returns the ACF values along with the associated lag in a tibble format. We have 601 autocorrelation (one for the time series and it’s 600 lags). All looks good.
max_lag <- 12 * 50
sun_spots %>%
tidy_acf(value, lags = 0:max_lag)
## # A tibble: 601 x 2
## lag acf
## <dbl> <dbl>
## 1 0. 1.00
## 2 1. 0.923
## 3 2. 0.893
## 4 3. 0.878
## 5 4. 0.867
## 6 5. 0.853
## 7 6. 0.840
## 8 7. 0.822
## 9 8. 0.809
## 10 9. 0.799
## # ... with 591 more rows
Let’s plot the ACF with ggplot2 to determine if a high-autocorrelation lag exists beyond 10 years.
sun_spots %>%
tidy_acf(value, lags = 0:max_lag) %>%
ggplot(aes(lag, acf)) +
geom_segment(aes(xend = lag, yend = 0), color = palette_light()[[1]]) +
geom_vline(xintercept = 120, size = 3, color = palette_light()[[2]]) +
annotate("text", label = "10 Year Mark", x = 130, y = 0.8,
color = palette_light()[[2]], size = 6, hjust = 0) +
theme_tq() +
labs(title = "ACF: Sunspots")
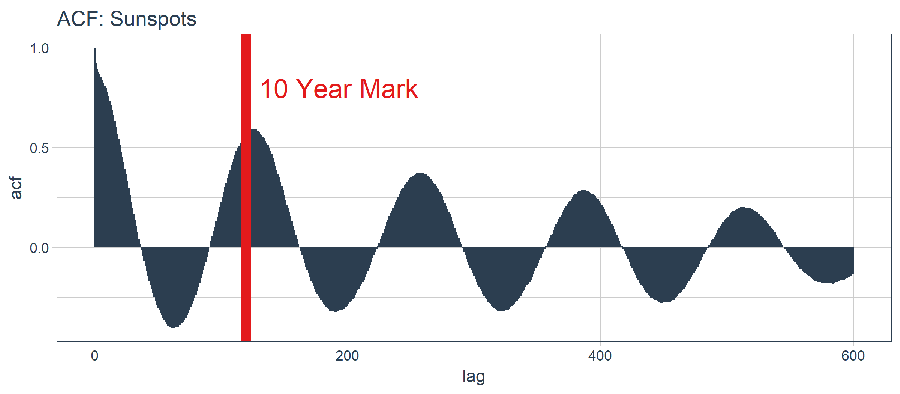
This is good news. We have autocorrelation in excess of 0.5 beyond lag 120 (the 10-year mark). We can theoretically use one of the high autocorrelation lags to develop an LSTM model.
sun_spots %>%
tidy_acf(value, lags = 115:135) %>%
ggplot(aes(lag, acf)) +
geom_vline(xintercept = 120, size = 3, color = palette_light()[[2]]) +
geom_segment(aes(xend = lag, yend = 0), color = palette_light()[[1]]) +
geom_point(color = palette_light()[[1]], size = 2) +
geom_label(aes(label = acf %>% round(2)), vjust = -1,
color = palette_light()[[1]]) +
annotate("text", label = "10 Year Mark", x = 121, y = 0.8,
color = palette_light()[[2]], size = 5, hjust = 0) +
theme_tq() +
labs(title = "ACF: Sunspots",
subtitle = "Zoomed in on Lags 115 to 135")
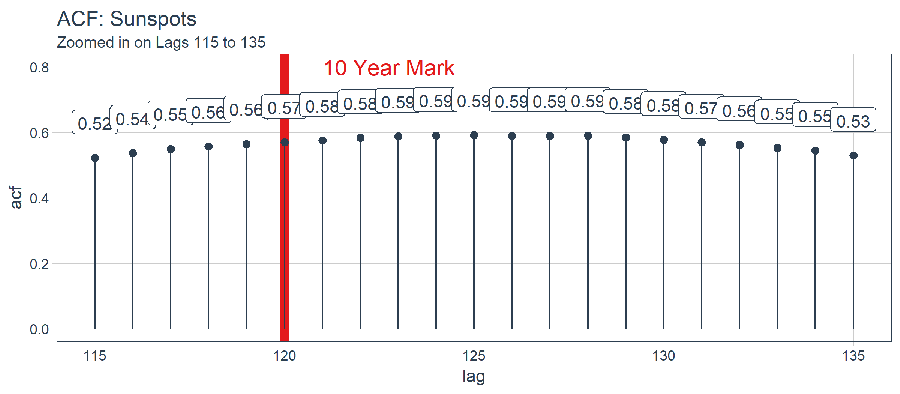
Upon inspection, the optimal lag occurs at lag 125. This isn’t necessarily the one we will use since we have more to consider with batch forecasting with a Keras LSTM. With that said, here’s how you can filter() to get the best lag.
optimal_lag_setting <- sun_spots %>%
tidy_acf(value, lags = 115:135) %>%
filter(acf == max(acf)) %>%
pull(lag)
optimal_lag_setting
## [1] 125
4.0 Backtesting: Time Series Cross Validation
Cross validation is the process of developing models on sub-sampled data against a validation set with the goal of determining an expected accuracy level and error range. Time series is a bit different than non-sequential data when it comes to cross validation. Specifically, the time dependency on previous time samples must be preserved when developing a sampling plan. We can create a cross validation sampling plan using by offsetting the window used to select sequential sub-samples. In finance, this type of analysis is often called “Backtesting”, which takes a time series and splits it into multiple uninterupted sequences offset at various windows that can be tested for strategies on both current and past observations.
A recent development is the rsample package, which makes cross validation sampling plans very easy to implement. Further, the rsample package has Backtesting covered. The vignette, “Time Series Analysis Example”, describes a procedure that uses the rolling_origin() function to create samples designed for time series cross validation. We’ll use this approach.
4.1 Developing A Backtesting Strategy
The sampling plan we create uses 50 years (initial = 12 x 50 samples) for the training set and ten years (assess = 12 x 10) for the testing (validation) set. We select a skip span of twenty years (skip = 12 x 20) to evenly distribute the samples into 11 sets that span the entire 265 years of sunspots history. Last, we select cumulative = FALSE to allow the origin to shift which ensures that models on more recent data are not given an unfair advantage (more observations) that those on less recent data. The tibble return contains the rolling_origin_resamples.
periods_train <- 12 * 50
periods_test <- 12 * 10
skip_span <- 12 * 20
rolling_origin_resamples <- rolling_origin(
sun_spots,
initial = periods_train,
assess = periods_test,
cumulative = FALSE,
skip = skip_span
)
rolling_origin_resamples
## # Rolling origin forecast resampling
## # A tibble: 11 x 2
## splits id
## <list> <chr>
## 1 <S3: rsplit> Slice01
## 2 <S3: rsplit> Slice02
## 3 <S3: rsplit> Slice03
## 4 <S3: rsplit> Slice04
## 5 <S3: rsplit> Slice05
## 6 <S3: rsplit> Slice06
## 7 <S3: rsplit> Slice07
## 8 <S3: rsplit> Slice08
## 9 <S3: rsplit> Slice09
## 10 <S3: rsplit> Slice10
## 11 <S3: rsplit> Slice11
4.2 Visualizing The Backtesting Strategy
We can visualize the resamples with two custom functions. The first, plot_split(), plots one of the resampling splits using ggplot2. Note that an expand_y_axis argument is added to expand the date range to the full sun_spots dataset date range. This will become useful when we visualize all plots together.
# Plotting function for a single split
plot_split <- function(split, expand_y_axis = TRUE, alpha = 1, size = 1, base_size = 14) {
# Manipulate data
train_tbl <- training(split) %>%
add_column(key = "training")
test_tbl <- testing(split) %>%
add_column(key = "testing")
data_manipulated <- bind_rows(train_tbl, test_tbl) %>%
as_tbl_time(index = index) %>%
mutate(key = fct_relevel(key, "training", "testing"))
# Collect attributes
train_time_summary <- train_tbl %>%
tk_index() %>%
tk_get_timeseries_summary()
test_time_summary <- test_tbl %>%
tk_index() %>%
tk_get_timeseries_summary()
# Visualize
g <- data_manipulated %>%
ggplot(aes(x = index, y = value, color = key)) +
geom_line(size = size, alpha = alpha) +
theme_tq(base_size = base_size) +
scale_color_tq() +
labs(
title = glue("Split: {split$id}"),
subtitle = glue("{train_time_summary$start} to {test_time_summary$end}"),
y = "", x = ""
) +
theme(legend.position = "none")
if (expand_y_axis) {
sun_spots_time_summary <- sun_spots %>%
tk_index() %>%
tk_get_timeseries_summary()
g <- g +
scale_x_date(limits = c(sun_spots_time_summary$start,
sun_spots_time_summary$end))
}
return(g)
}
The plot_split() function takes one split (in this case Slice01), and returns a visual of the sampling strategy. We expand the axis to the range for the full dataset using expand_y_axis = TRUE.
rolling_origin_resamples$splits[[1]] %>%
plot_split(expand_y_axis = TRUE) +
theme(legend.position = "bottom")

The second function, plot_sampling_plan(), scales the plot_split() function to all of the samples using purrr and cowplot.
# Plotting function that scales to all splits
plot_sampling_plan <- function(sampling_tbl, expand_y_axis = TRUE,
ncol = 3, alpha = 1, size = 1, base_size = 14,
title = "Sampling Plan") {
# Map plot_split() to sampling_tbl
sampling_tbl_with_plots <- sampling_tbl %>%
mutate(gg_plots = map(splits, plot_split,
expand_y_axis = expand_y_axis,
alpha = alpha, base_size = base_size))
# Make plots with cowplot
plot_list <- sampling_tbl_with_plots$gg_plots
p_temp <- plot_list[[1]] + theme(legend.position = "bottom")
legend <- get_legend(p_temp)
p_body <- plot_grid(plotlist = plot_list, ncol = ncol)
p_title <- ggdraw() +
draw_label(title, size = 18, fontface = "bold", colour = palette_light()[[1]])
g <- plot_grid(p_title, p_body, legend, ncol = 1, rel_heights = c(0.05, 1, 0.05))
return(g)
}
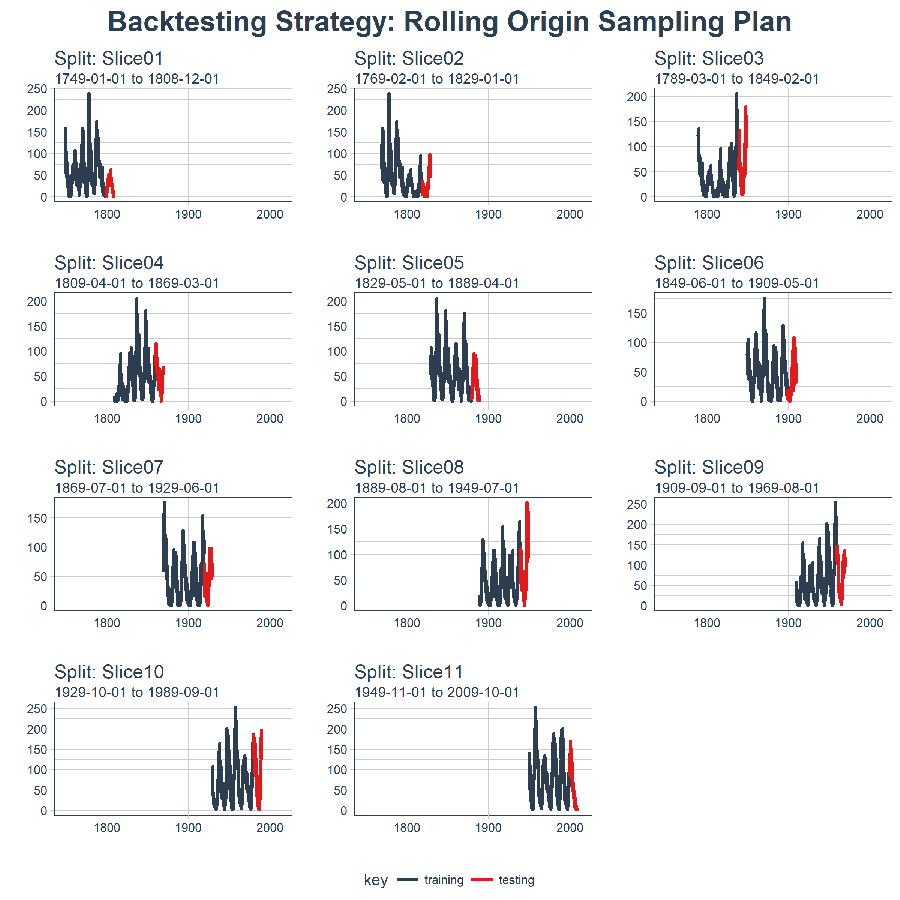
We can now visualize the ENTIRE BACKTESTING STRATEGY with plot_sampling_plan()! We can see how the sampling plan shifts the sampling window with each progressive slice of the train/test splits.
rolling_origin_resamples %>%
plot_sampling_plan(expand_y_axis = T, ncol = 3, alpha = 1, size = 1, base_size = 10,
title = "Backtesting Strategy: Rolling Origin Sampling Plan")
And, we can set expand_y_axis = FALSE to zoom in on the samples.
rolling_origin_resamples %>%
plot_sampling_plan(expand_y_axis = F, ncol = 3, alpha = 1, size = 1, base_size = 10,
title = "Backtesting Strategy: Zoomed In")
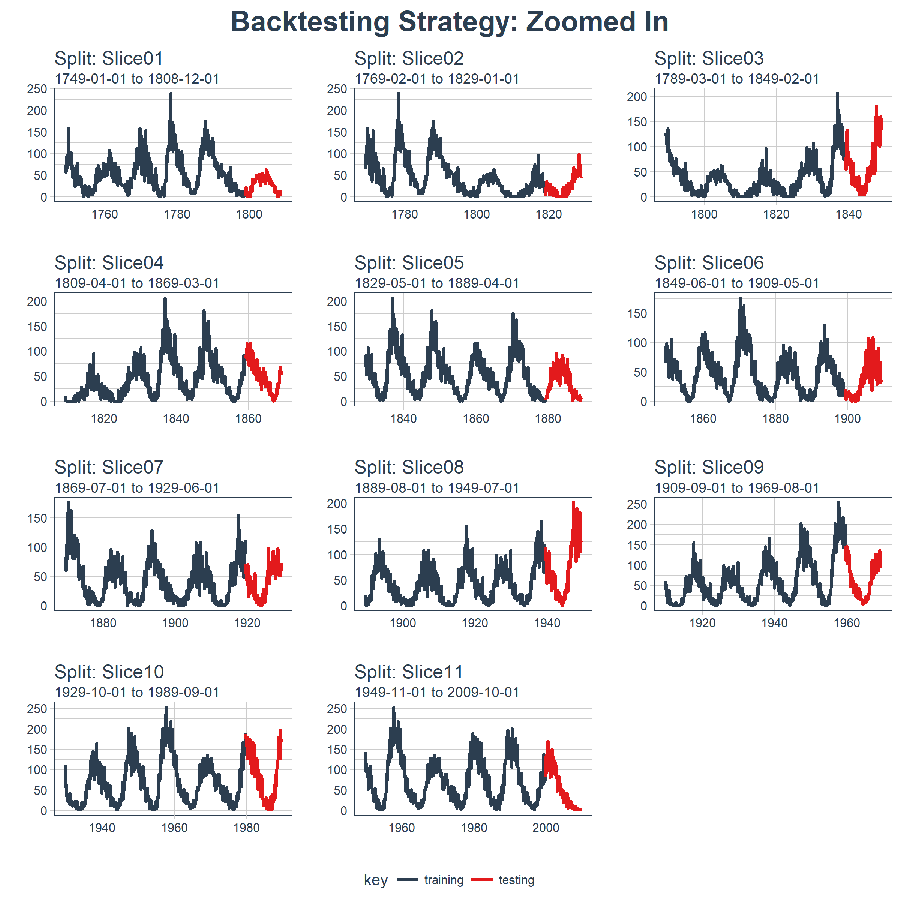
We’ll use this Backtesting Strategy (11 samples from one time series each with 50/10 split in years and a 20 year offset) when testing the veracity of the LSTM model on the sunspots dataset.
5.0 Modeling The Keras Stateful LSTM Model
To begin, we’ll develop a single Keras Stateful LSTM model on a single sample from the Backtesting Strategy. We’ll then scale the model to all samples to investigate/validate the modeling performance.
5.1 Single LSTM
For the single LSTM model, we’ll select and visualize the split for the most recent time sample/slice (Slice11). The 11th split contains the most recent data.
split <- rolling_origin_resamples$splits[[11]]
split_id <- rolling_origin_resamples$id[[11]]
5.1.1 Visualizing The Split
We can reuse the plot_split() function to visualize the split. Set expand_y_axis = FALSE to zoom in on the subsample.
plot_split(split, expand_y_axis = FALSE, size = 0.5) +
theme(legend.position = "bottom") +
ggtitle(glue("Split: {split_id}"))
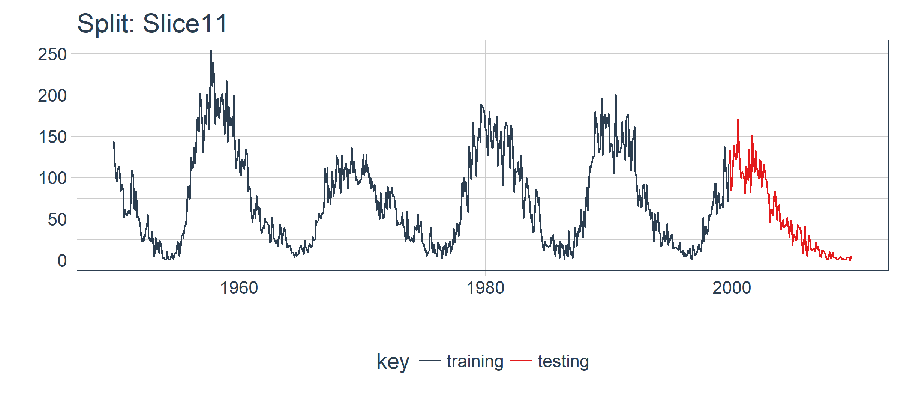
5.1.2 Data Setup
First, let’s combine the training and testing data sets into a single data set with a column key that specifies what set they came from (either “training” or “testing)”. Note that the tbl_time object will need to have the index re-specified during the bind_rows() step, but this issue should be corrected in dplyr soon (please upvote it so RStudio focuses on it).
df_trn <- training(split)
df_tst <- testing(split)
df <- bind_rows(
df_trn %>% add_column(key = "training"),
df_tst %>% add_column(key = "testing")
) %>%
as_tbl_time(index = index)
df
## # A time tibble: 720 x 3
## # Index: index
## index value key
## <date> <dbl> <chr>
## 1 1949-11-01 144. training
## 2 1949-12-01 118. training
## 3 1950-01-01 102. training
## 4 1950-02-01 94.8 training
## 5 1950-03-01 110. training
## 6 1950-04-01 113. training
## 7 1950-05-01 106. training
## 8 1950-06-01 83.6 training
## 9 1950-07-01 91.0 training
## 10 1950-08-01 85.2 training
## # ... with 710 more rows
5.1.3 Preprocessing With Recipes
The LSTM algorithm requires the input data to be centered and scaled. We can preprocess the data using the recipes package. We’ll use a combination of step_sqrt to transform the data and reduce the presence of outliers and step_center and step_scale to center and scale the data. The data is processed/transformed using the bake() function.
rec_obj <- recipe(value ~ ., df) %>%
step_sqrt(value) %>%
step_center(value) %>%
step_scale(value) %>%
prep()
df_processed_tbl <- bake(rec_obj, df)
df_processed_tbl
## # A tibble: 720 x 3
## index value key
## <date> <dbl> <fct>
## 1 1949-11-01 1.25 training
## 2 1949-12-01 0.929 training
## 3 1950-01-01 0.714 training
## 4 1950-02-01 0.617 training
## 5 1950-03-01 0.825 training
## 6 1950-04-01 0.874 training
## 7 1950-05-01 0.777 training
## 8 1950-06-01 0.450 training
## 9 1950-07-01 0.561 training
## 10 1950-08-01 0.474 training
## # ... with 710 more rows
Next, let’s capture the center/scale history so we can invert the center and scaling after modeling. The square-root transformation can be inverted by squaring the inverted center/scale values.
center_history <- rec_obj$steps[[2]]$means["value"]
scale_history <- rec_obj$steps[[3]]$sds["value"]
c("center" = center_history, "scale" = scale_history)
## center.value scale.value
## 7.549526 3.545561
5.1.4 LSTM Plan
We need a plan for building the LSTM. First, a couple PRO TIPS with LSTM’s:
Tensor Format:
- Predictors (X) must be a 3D Array with dimensions: [samples, timesteps, features]: The first dimension is the length of values, the second is the number of time steps (lags), and the third is the number of predictors (1 if univariate or n if multivariate)
- Outcomes/Targets (y) must be a 2D Array with dimensions: [samples, timesteps]: The first dimension is the length of values and the second is the number of time steps (lags)
Training/Testing:
- The training and testing length must be evenly divisible (e.g. training length / testing length must be a whole number)
Batch Size:
- The batch size is the number of training examples in one forward/backward pass of a RNN before a weight update
- The batch size must be evenly divisible into both the training an testing lengths (e.g. training length / batch size and testing length / batch size must both be whole numbers)
Time Steps:
- A time step is the number of lags included in the training/testing set
- For our example, our we use a single lag
Epochs:
- The epochs are the total number of forward/backward pass iterations
- Typically more improves model performance unless overfitting occurs at which time the validation accuracy/loss will not improve
Taking this in, we can come up with a plan. We’ll select a prediction of window 120 months (10 years) or the length of our test set. The best correlation occurs at 125, but this is not evenly divisible by the forecasting range. We could increase the forecast horizon, but this offers a minimal increase in autocorrelation. We can select a batch size of 40 units which evenly divides into the number of testing and training observations. We select time steps = 1, which is because we are only using one lag. Finally, we set epochs = 300, but this will need to be adjusted to balance the bias/variance tradeoff.
# Model inputs
lag_setting <- 120 # = nrow(df_tst)
batch_size <- 40
train_length <- 440
tsteps <- 1
epochs <- 300
5.1.5 2D And 3D Train/Test Arrays
We can then setup the training and testing sets in the correct format (arrays) as follows. Remember, LSTM’s need 3D arrays for predictors (X) and 2D arrays for outcomes/targets (y).
# Training Set
lag_train_tbl <- df_processed_tbl %>%
mutate(value_lag = lag(value, n = lag_setting)) %>%
filter(!is.na(value_lag)) %>%
filter(key == "training") %>%
tail(train_length)
x_train_vec <- lag_train_tbl$value_lag
x_train_arr <- array(data = x_train_vec, dim = c(length(x_train_vec), 1, 1))
y_train_vec <- lag_train_tbl$value
y_train_arr <- array(data = y_train_vec, dim = c(length(y_train_vec), 1))
# Testing Set
lag_test_tbl <- df_processed_tbl %>%
mutate(
value_lag = lag(value, n = lag_setting)
) %>%
filter(!is.na(value_lag)) %>%
filter(key == "testing")
x_test_vec <- lag_test_tbl$value_lag
x_test_arr <- array(data = x_test_vec, dim = c(length(x_test_vec), 1, 1))
y_test_vec <- lag_test_tbl$value
y_test_arr <- array(data = y_test_vec, dim = c(length(y_test_vec), 1))
5.1.6 Building The LSTM Model
We can build an LSTM model using the keras_model_sequential() and adding layers like stacking bricks. We’ll use two LSTM layers each with 50 units. The first LSTM layer takes the required input shape, which is the [time steps, number of features]. The batch size is just our batch size. We set the first layer to return_sequences = TRUE and stateful = TRUE. The second layer is the same with the exception of batch_size, which only needs to be specified in the first layer, and return_sequences = FALSE which does not return the time stamp dimension (2D shape is returned versus a 3D shape from the first LSTM). We tack on a layer_dense(units = 1), which is the standard ending to a keras sequential model. Last, we compile() using the loss = "mae" and the popular optimizer = "adam".
model <- keras_model_sequential()
model %>%
layer_lstm(units = 50,
input_shape = c(tsteps, 1),
batch_size = batch_size,
return_sequences = TRUE,
stateful = TRUE) %>%
layer_lstm(units = 50,
return_sequences = FALSE,
stateful = TRUE) %>%
layer_dense(units = 1)
model %>%
compile(loss = 'mae', optimizer = 'adam')
model
## Model
## ______________________________________________________________________
## Layer (type) Output Shape Param #
## ======================================================================
## lstm_1 (LSTM) (40, 1, 50) 10400
## ______________________________________________________________________
## lstm_2 (LSTM) (40, 50) 20200
## ______________________________________________________________________
## dense_1 (Dense) (40, 1) 51
## ======================================================================
## Total params: 30,651
## Trainable params: 30,651
## Non-trainable params: 0
## ______________________________________________________________________
5.1.7 Fitting The LSTM Model
Next, we can fit our stateful LSTM using a for loop (we do this to manually reset states). This will take a minute or so for 300 epochs to run. We set shuffle = FALSE to preserve sequences, and we manually reset the states after each epoch using reset_states().
for (i in 1:epochs) {
model %>% fit(x = x_train_arr,
y = y_train_arr,
batch_size = batch_size,
epochs = 1,
verbose = 1,
shuffle = FALSE)
model %>% reset_states()
cat("Epoch: ", i)
}
5.1.8 Predicting Using The LSTM Model
We can then make predictions on the test set, x_test_arr, using the predict() function. We can retransform our predictions using the scale_history and center_history, which were previously saved and then squaring the result. Finally, we combine the predictions with the original data in one column using reduce() and a custom time_bind_rows() function.
# Make Predictions
pred_out <- model %>%
predict(x_test_arr, batch_size = batch_size) %>%
.[,1]
# Retransform values
pred_tbl <- tibble(
index = lag_test_tbl$index,
value = (pred_out * scale_history + center_history)^2
)
# Combine actual data with predictions
tbl_1 <- df_trn %>%
add_column(key = "actual")
tbl_2 <- df_tst %>%
add_column(key = "actual")
tbl_3 <- pred_tbl %>%
add_column(key = "predict")
# Create time_bind_rows() to solve dplyr issue
time_bind_rows <- function(data_1, data_2, index) {
index_expr <- enquo(index)
bind_rows(data_1, data_2) %>%
as_tbl_time(index = !! index_expr)
}
ret <- list(tbl_1, tbl_2, tbl_3) %>%
reduce(time_bind_rows, index = index) %>%
arrange(key, index) %>%
mutate(key = as_factor(key))
ret
## # A time tibble: 840 x 3
## # Index: index
## index value key
## <date> <dbl> <fct>
## 1 1949-11-01 144. actual
## 2 1949-12-01 118. actual
## 3 1950-01-01 102. actual
## 4 1950-02-01 94.8 actual
## 5 1950-03-01 110. actual
## 6 1950-04-01 113. actual
## 7 1950-05-01 106. actual
## 8 1950-06-01 83.6 actual
## 9 1950-07-01 91.0 actual
## 10 1950-08-01 85.2 actual
## # ... with 830 more rows
We can use the yardstick package to assess performance using the rmse() function, which returns the root mean squared error (RMSE). Our data is in the long format (optimal format for visualizing with ggplot2), so we’ll create a wrapper function calc_rmse() that processes the data into the format needed for yardstick::rmse().
calc_rmse <- function(prediction_tbl) {
rmse_calculation <- function(data) {
data %>%
spread(key = key, value = value) %>%
select(-index) %>%
filter(!is.na(predict)) %>%
rename(
truth = actual,
estimate = predict
) %>%
rmse(truth, estimate)
}
safe_rmse <- possibly(rmse_calculation, otherwise = NA)
safe_rmse(prediction_tbl)
}
We can inspect the RMSE on the model.
calc_rmse(ret)
## [1] 31.81798
The RMSE doesn’t tell us the story. We need to visualize. Note - The RMSE will come in handy in determining an expected error when we scale to all samples in the backtesting strategy.
5.1.10 Visualizing The Single Prediction
Next, we make a plotting function, plot_prediction(), using ggplot2 to visualize the results for a single sample.
# Setup single plot function
plot_prediction <- function(data, id, alpha = 1, size = 2, base_size = 14) {
rmse_val <- calc_rmse(data)
g <- data %>%
ggplot(aes(index, value, color = key)) +
geom_point(alpha = alpha, size = size) +
theme_tq(base_size = base_size) +
scale_color_tq() +
theme(legend.position = "none") +
labs(
title = glue("{id}, RMSE: {round(rmse_val, digits = 1)}"),
x = "", y = ""
)
return(g)
}
We can test out the plotting function setting the id = split_id, which is “Slice11”.
ret %>%
plot_prediction(id = split_id, alpha = 0.65) +
theme(legend.position = "bottom")
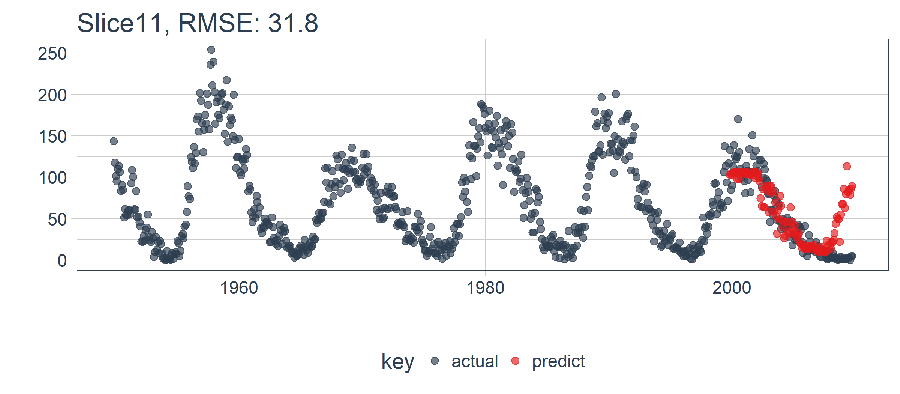
The LSTM performed relatively well! The settings we selected seem to produce a decent model that picked up the trend. It jumped the gun on the next up-trend, but overall it exceeded my expectations. Now, we need to Backtest to see the true performance over time!
5.2 Backtesting The LSTM On All Eleven Samples
Once we have the LSTM working for one sample, scaling to all 11 is relatively simple. We just need to create an prediction function that can be mapped to the sampling plan data contained in rolling_origin_resamples.
5.2.1 Creating An LSTM Prediction Function
This step looks intimidating, but it’s actually straightforward. We copy the code from Section 5.1 - Single LSTM into a function. We’ll make it a safe function, which is a good practice for any long-running mapping processes to prevent a single failure from stopping the entire process.
predict_keras_lstm <- function(split, epochs = 300, ...) {
lstm_prediction <- function(split, epochs, ...) {
# 5.1.2 Data Setup
df_trn <- training(split)
df_tst <- testing(split)
df <- bind_rows(
df_trn %>% add_column(key = "training"),
df_tst %>% add_column(key = "testing")
) %>%
as_tbl_time(index = index)
# 5.1.3 Preprocessing
rec_obj <- recipe(value ~ ., df) %>%
step_sqrt(value) %>%
step_center(value) %>%
step_scale(value) %>%
prep()
df_processed_tbl <- bake(rec_obj, df)
center_history <- rec_obj$steps[[2]]$means["value"]
scale_history <- rec_obj$steps[[3]]$sds["value"]
# 5.1.4 LSTM Plan
lag_setting <- 120 # = nrow(df_tst)
batch_size <- 40
train_length <- 440
tsteps <- 1
epochs <- epochs
# 5.1.5 Train/Test Setup
lag_train_tbl <- df_processed_tbl %>%
mutate(value_lag = lag(value, n = lag_setting)) %>%
filter(!is.na(value_lag)) %>%
filter(key == "training") %>%
tail(train_length)
x_train_vec <- lag_train_tbl$value_lag
x_train_arr <- array(data = x_train_vec, dim = c(length(x_train_vec), 1, 1))
y_train_vec <- lag_train_tbl$value
y_train_arr <- array(data = y_train_vec, dim = c(length(y_train_vec), 1))
lag_test_tbl <- df_processed_tbl %>%
mutate(
value_lag = lag(value, n = lag_setting)
) %>%
filter(!is.na(value_lag)) %>%
filter(key == "testing")
x_test_vec <- lag_test_tbl$value_lag
x_test_arr <- array(data = x_test_vec, dim = c(length(x_test_vec), 1, 1))
y_test_vec <- lag_test_tbl$value
y_test_arr <- array(data = y_test_vec, dim = c(length(y_test_vec), 1))
# 5.1.6 LSTM Model
model <- keras_model_sequential()
model %>%
layer_lstm(units = 50,
input_shape = c(tsteps, 1),
batch_size = batch_size,
return_sequences = TRUE,
stateful = TRUE) %>%
layer_lstm(units = 50,
return_sequences = FALSE,
stateful = TRUE) %>%
layer_dense(units = 1)
model %>%
compile(loss = 'mae', optimizer = 'adam')
# 5.1.7 Fitting LSTM
for (i in 1:epochs) {
model %>% fit(x = x_train_arr,
y = y_train_arr,
batch_size = batch_size,
epochs = 1,
verbose = 1,
shuffle = FALSE)
model %>% reset_states()
cat("Epoch: ", i)
}
# 5.1.8 Predict and Return Tidy Data
# Make Predictions
pred_out <- model %>%
predict(x_test_arr, batch_size = batch_size) %>%
.[,1]
# Retransform values
pred_tbl <- tibble(
index = lag_test_tbl$index,
value = (pred_out * scale_history + center_history)^2
)
# Combine actual data with predictions
tbl_1 <- df_trn %>%
add_column(key = "actual")
tbl_2 <- df_tst %>%
add_column(key = "actual")
tbl_3 <- pred_tbl %>%
add_column(key = "predict")
# Create time_bind_rows() to solve dplyr issue
time_bind_rows <- function(data_1, data_2, index) {
index_expr <- enquo(index)
bind_rows(data_1, data_2) %>%
as_tbl_time(index = !! index_expr)
}
ret <- list(tbl_1, tbl_2, tbl_3) %>%
reduce(time_bind_rows, index = index) %>%
arrange(key, index) %>%
mutate(key = as_factor(key))
return(ret)
}
safe_lstm <- possibly(lstm_prediction, otherwise = NA)
safe_lstm(split, epochs, ...)
}
We can test the custom predict_keras_lstm() function out with 10 epochs. It returns the data in long format with “actual” and “predict” values in the key column.
predict_keras_lstm(split, epochs = 10)
## # A time tibble: 840 x 3
## # Index: index
## index value key
## <date> <dbl> <fct>
## 1 1949-11-01 144. actual
## 2 1949-12-01 118. actual
## 3 1950-01-01 102. actual
## 4 1950-02-01 94.8 actual
## 5 1950-03-01 110. actual
## 6 1950-04-01 113. actual
## 7 1950-05-01 106. actual
## 8 1950-06-01 83.6 actual
## 9 1950-07-01 91.0 actual
## 10 1950-08-01 85.2 actual
## # ... with 830 more rows
5.2.2 Mapping The LSTM Prediction Function Over The 11 Samples
With the predict_keras_lstm() function in hand that works on one split, we can now map to all samples using a mutate() and map() combo. The predictions will be stored in a “list” column called “predict”. Note that this will take 5-10 minutes or so to complete.
sample_predictions_lstm_tbl <- rolling_origin_resamples %>%
mutate(predict = map(splits, predict_keras_lstm, epochs = 300))
We now have the predictions in the column “predict” for all 11 splits!.
sample_predictions_lstm_tbl
## # Rolling origin forecast resampling
## # A tibble: 11 x 3
## splits id predict
## * <list> <chr> <list>
## 1 <S3: rsplit> Slice01 <tibble [840 x 3]>
## 2 <S3: rsplit> Slice02 <tibble [840 x 3]>
## 3 <S3: rsplit> Slice03 <tibble [840 x 3]>
## 4 <S3: rsplit> Slice04 <tibble [840 x 3]>
## 5 <S3: rsplit> Slice05 <tibble [840 x 3]>
## 6 <S3: rsplit> Slice06 <tibble [840 x 3]>
## 7 <S3: rsplit> Slice07 <tibble [840 x 3]>
## 8 <S3: rsplit> Slice08 <tibble [840 x 3]>
## 9 <S3: rsplit> Slice09 <tibble [840 x 3]>
## 10 <S3: rsplit> Slice10 <tibble [840 x 3]>
## 11 <S3: rsplit> Slice11 <tibble [840 x 3]>
We can assess the RMSE by mapping the calc_rmse() function to the “predict” column.
sample_rmse_tbl <- sample_predictions_lstm_tbl %>%
mutate(rmse = map_dbl(predict, calc_rmse)) %>%
select(id, rmse)
sample_rmse_tbl
## # Rolling origin forecast resampling
## # A tibble: 11 x 2
## id rmse
## * <chr> <dbl>
## 1 Slice01 48.2
## 2 Slice02 17.4
## 3 Slice03 41.0
## 4 Slice04 26.6
## 5 Slice05 22.2
## 6 Slice06 49.0
## 7 Slice07 18.1
## 8 Slice08 54.9
## 9 Slice09 28.0
## 10 Slice10 38.4
## 11 Slice11 34.2
sample_rmse_tbl %>%
ggplot(aes(rmse)) +
geom_histogram(aes(y = ..density..), fill = palette_light()[[1]], bins = 16) +
geom_density(fill = palette_light()[[1]], alpha = 0.5) +
theme_tq() +
ggtitle("Histogram of RMSE")
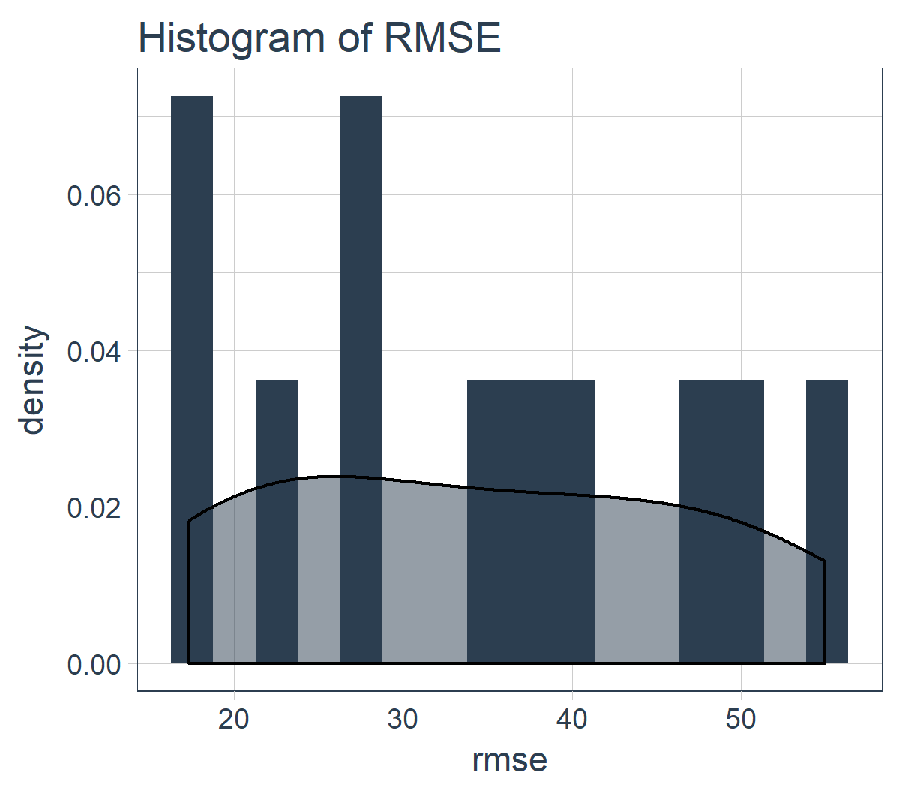
And, we can summarize the RMSE for the 11 slices. PRO TIP: Using the average and standard deviation of the RMSE (or other similar metric) is a good way to compare the performance of various models.
sample_rmse_tbl %>%
summarize(
mean_rmse = mean(rmse),
sd_rmse = sd(rmse)
)
## # Rolling origin forecast resampling
## # A tibble: 1 x 2
## mean_rmse sd_rmse
## <dbl> <dbl>
## 1 34.4 13.0
5.2.4 Visualizing The Backtest Results
We can create a plot_predictions() function that returns one plot with the predictions for the entire set of 11 backtesting samples!!!
plot_predictions <- function(sampling_tbl, predictions_col,
ncol = 3, alpha = 1, size = 2, base_size = 14,
title = "Backtested Predictions") {
predictions_col_expr <- enquo(predictions_col)
# Map plot_split() to sampling_tbl
sampling_tbl_with_plots <- sampling_tbl %>%
mutate(gg_plots = map2(!! predictions_col_expr, id,
.f = plot_prediction,
alpha = alpha,
size = size,
base_size = base_size))
# Make plots with cowplot
plot_list <- sampling_tbl_with_plots$gg_plots
p_temp <- plot_list[[1]] + theme(legend.position = "bottom")
legend <- get_legend(p_temp)
p_body <- plot_grid(plotlist = plot_list, ncol = ncol)
p_title <- ggdraw() +
draw_label(title, size = 18, fontface = "bold", colour = palette_light()[[1]])
g <- plot_grid(p_title, p_body, legend, ncol = 1, rel_heights = c(0.05, 1, 0.05))
return(g)
}
Here’s the result. On a data set that’s not easy to predict, this is quite impressive!!
sample_predictions_lstm_tbl %>%
plot_predictions(predictions_col = predict, alpha = 0.5, size = 1, base_size = 10,
title = "Keras Stateful LSTM: Backtested Predictions")
5.3 Predicting The Next 10 Years
We can predict the next 10 years by adjusting the prediction function to work with the full data set. A new function, predict_keras_lstm_future(), is created that predicts the next 120 time steps (or ten years).
predict_keras_lstm_future <- function(data, epochs = 300, ...) {
lstm_prediction <- function(data, epochs, ...) {
# 5.1.2 Data Setup (MODIFIED)
df <- data
# 5.1.3 Preprocessing
rec_obj <- recipe(value ~ ., df) %>%
step_sqrt(value) %>%
step_center(value) %>%
step_scale(value) %>%
prep()
df_processed_tbl <- bake(rec_obj, df)
center_history <- rec_obj$steps[[2]]$means["value"]
scale_history <- rec_obj$steps[[3]]$sds["value"]
# 5.1.4 LSTM Plan
lag_setting <- 120 # = nrow(df_tst)
batch_size <- 40
train_length <- 440
tsteps <- 1
epochs <- epochs
# 5.1.5 Train Setup (MODIFIED)
lag_train_tbl <- df_processed_tbl %>%
mutate(value_lag = lag(value, n = lag_setting)) %>%
filter(!is.na(value_lag)) %>%
tail(train_length)
x_train_vec <- lag_train_tbl$value_lag
x_train_arr <- array(data = x_train_vec, dim = c(length(x_train_vec), 1, 1))
y_train_vec <- lag_train_tbl$value
y_train_arr <- array(data = y_train_vec, dim = c(length(y_train_vec), 1))
x_test_vec <- y_train_vec %>% tail(lag_setting)
x_test_arr <- array(data = x_test_vec, dim = c(length(x_test_vec), 1, 1))
# 5.1.6 LSTM Model
model <- keras_model_sequential()
model %>%
layer_lstm(units = 50,
input_shape = c(tsteps, 1),
batch_size = batch_size,
return_sequences = TRUE,
stateful = TRUE) %>%
layer_lstm(units = 50,
return_sequences = FALSE,
stateful = TRUE) %>%
layer_dense(units = 1)
model %>%
compile(loss = 'mae', optimizer = 'adam')
# 5.1.7 Fitting LSTM
for (i in 1:epochs) {
model %>% fit(x = x_train_arr,
y = y_train_arr,
batch_size = batch_size,
epochs = 1,
verbose = 1,
shuffle = FALSE)
model %>% reset_states()
cat("Epoch: ", i)
}
# 5.1.8 Predict and Return Tidy Data (MODIFIED)
# Make Predictions
pred_out <- model %>%
predict(x_test_arr, batch_size = batch_size) %>%
.[,1]
# Make future index using tk_make_future_timeseries()
idx <- data %>%
tk_index() %>%
tk_make_future_timeseries(n_future = lag_setting)
# Retransform values
pred_tbl <- tibble(
index = idx,
value = (pred_out * scale_history + center_history)^2
)
# Combine actual data with predictions
tbl_1 <- df %>%
add_column(key = "actual")
tbl_3 <- pred_tbl %>%
add_column(key = "predict")
# Create time_bind_rows() to solve dplyr issue
time_bind_rows <- function(data_1, data_2, index) {
index_expr <- enquo(index)
bind_rows(data_1, data_2) %>%
as_tbl_time(index = !! index_expr)
}
ret <- list(tbl_1, tbl_3) %>%
reduce(time_bind_rows, index = index) %>%
arrange(key, index) %>%
mutate(key = as_factor(key))
return(ret)
}
safe_lstm <- possibly(lstm_prediction, otherwise = NA)
safe_lstm(data, epochs, ...)
}
Next, run predict_keras_lstm_future() on the sun_spots data set.
future_sun_spots_tbl <- predict_keras_lstm_future(sun_spots, epochs = 300)
Last, we can visualize the forecast with the plot_prediction() function, setting id = NULL. We can use filter_time() to zoom in on the dataset since 1900.
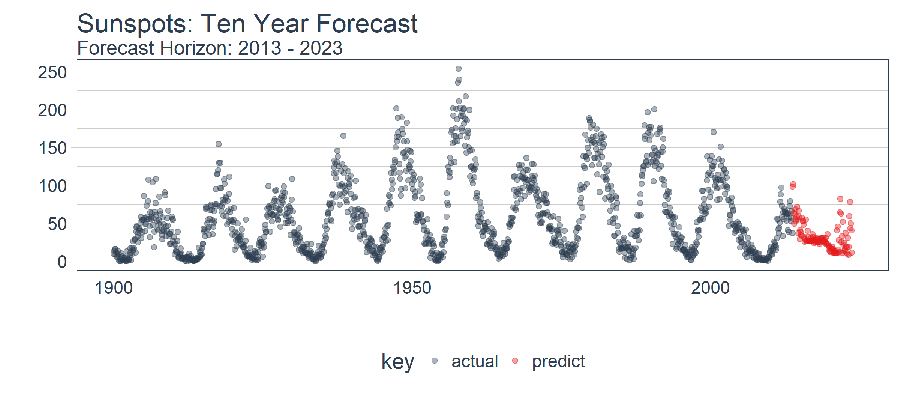
future_sun_spots_tbl %>%
filter_time("1900" ~ "end") %>%
plot_prediction(id = NULL, alpha = 0.4, size = 1.5) +
theme(legend.position = "bottom") +
ggtitle("Sunspots: Ten Year Forecast", subtitle = "Forecast Horizon: 2013 - 2023")
Conclusions
This article demonstrates the power of a Stateful LSTM built using the keras package. It’s surprising how well the deep learning approach learned the trend given that the only feature provided was the lag at 120. The backtested model had an Average RMSE of 34 and a Standard Deviation RMSE of 13. While not shown in the article, we tested this against ARIMA and prophet, and the LSTM outperformed both by a more than 30% reduction in average error and 40% reduction in standard deviation. This shows the benefit of machine learning tool-application fit.
Beyond the deep learning approach used, the article also exposed methods to determine whether an LSTM is a good option for the given time series using ACF plot. We also exposed how the veracity of a time series model should be benchmarked by backtesting, a strategy that can be used for cross validation that preserves the sequential aspects of the time series.
Business Science University
Enjoy data science for business? We do too. This is why we created Business Science University where we teach you how to do Data Science For Busines (#DS4B) just like us!
Who is this course for?
Anyone that is interested in applying data science in a business context (we call this DS4B). All you need is basic R, dplyr, and ggplot2 experience. If you understood this article, you are qualified.
What do you get it out of it?
You learn everything you need to know about how to apply data science in a business context:
-
Using ROI-driven data science taught from consulting experience!
-
Solve high-impact problems (e.g. $15M Employee Attrition Problem)
-
Use advanced, bleeding-edge machine learning algorithms (e.g. H2O, LIME)
-
Apply systematic data science frameworks (e.g. Business Science Problem Framework)
New R Package: Anomalize For Scalable Time Series Anomaly Detection
We just released our package, anomalize. You can learn more from the Anomalize Documentation or by watching our 2-minute introductory video!
About Business Science
Business Science specializes in “ROI-driven data science”. We offer training, education, coding expertise, and data science consulting related to business and finance. Our latest creation is Business Science University, which is coming soon! In addition, we deliver about 80% of our effort into the open source data science community in the form of software and our Business Science blog. Visit Business Science on the web or contact us to learn more!
Don’t Miss A Beat
Connect With Business Science
If you like our software (anomalize, tidyquant, tibbletime, timetk, and sweep), our courses, and our company, you can connect with us: