Russell 2000 Quantitative Stock Analysis in R: Six Stocks with Amazing, Consistent Growth
Written
The Russell 2000 Small-Cap Index, ticker symbol: ^RUT, is the hottest index of 2016 with YTD gains of over 18%. The index components are interesting not only because of recent performance, but because the top performers either grow to become mid-cap stocks or are bought by large-cap companies at premium prices. This means selecting the best components can result in large gains. In this post, I’ll perform a quantitative stock analysis on the entire list of Russell 2000 stock components using the R programming language. Building on the methodology from my S&P Analysis Post, I develop screening and ranking metrics to identify the top stocks with amazing growth and most consistency. I use R for the analysis including the rvest library for web scraping the list of Russell 2000 stocks, quantmod to collect historical prices for all 2000+ stock components, purrr to map modeling functions, and various other tidyverse libraries such as ggplot2, dplyr, and tidyr to visualize and manage the data workflow. Last, I use plotly to create an interactive visualization used in the screening process. Whether you are familiar with quantitative stock analysis, just beginning, or just interested in the R programming language, you’ll gain both knowledge of data science in R and immediate insights into the best Russell 2000 stocks, quantitatively selected for future returns!
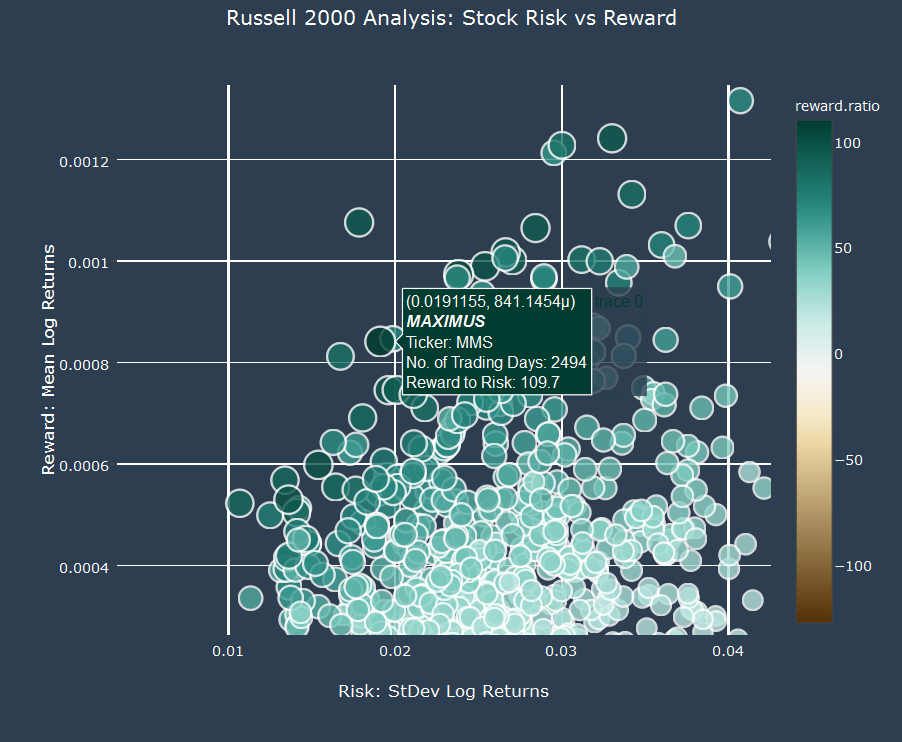
In part 1 of the analysis, we screen the entire stock list using a reward-to-risk metric. Here’s a sneak peek at the plotly interactive visualization, which aids in screening the stocks. The best stocks from the algorithm are those with highest reward.metric. The color and size varies with the value of the reward.metric. You can pan, zoom in, and hover over the points to gain information about the stocks.
In part 2 of the analysis, we review the top 15 stocks from part 1, developing a new, growth-to-consistency metric, to programmatically select the best of the best. Here’s a sneak peek at the top six stocks from the Russell 2000 index, with performance adjusted to remove stock splits.
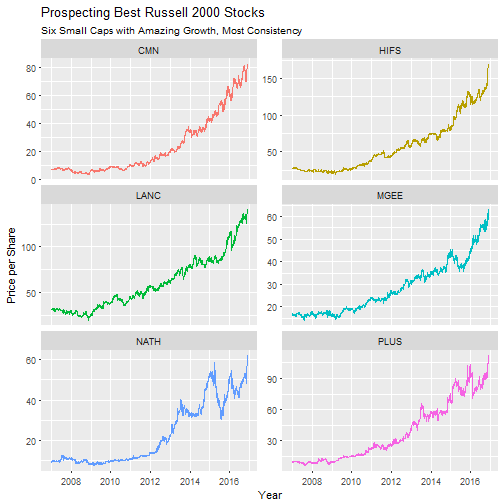
Table of Contents
Overview
The S&P500 Analysis Post covered the fundamentals of quantitative stock analysis. I’ll spare you the details, but if interested I strongly recommend going through that post to get up to speed. The methodology leverages the fact that stock returns are approximately normally distributed and uncorrelated. Because of this, we can model the behavior of stock prices within a confidence interval using the mean and standard deviation of the stock returns. The general process is to collect the historical stock prices, calculate the daily log returns (we use log returns for structural reasons), then calculate the mean and standard deviation of the log returns. The mean characterizes the growth rate (reward) and the standard deviation characterizes the volatility (risk).
In this post, we build on what where we left off in the S&P500 Analysis Post, this time taking the analysis to a new level using a new stock index: the Russell 2000 Small Cap Index. The Russell 2000 index is a perfect candidate because it’s 4X the size of the S&P500 index, it contains only small-cap stocks (median market cap of $528M), and it’s not as well known meaning it’s full of hidden gems and takeover targets. Plus, it’s up over 18% this year!
In part 1 of this analysis, we analyze the Russell 2000 stock list honing in on the relationship between the mean and standard deviation of daily log returns. From there, we develop a reward-to-risk metric based on how the market tends to treat stocks. The end result is a plotly interactive graph that enables visualizing the attributes of the best and worst stocks.
In part 2, we switch focus to the top 15 stocks from part 1, this time evaluating on how consistently each stock performs. We develop a new metric, growth-to-consistency which enables programmatically selecting the best stocks. We end by selecting the top 6 stocks with the unique combination of amazing growth, low volatility, and consistent returns.
The full code for the tutorial can be downloaded as a .R file here.
Prerequisites
For those following along in R, you’ll need to load the following packages:
library(rvest) # web scraping
library(quantmod) # get stock prices; useful stock analysis functions
library(tidyverse) # ggplot2, purrr, dplyr, tidyr, readr, tibble
library(stringr) # working with strings
library(modelr) # geom_ref_line() function
library(lubridate) # working with dates
library(plotly) # interactive plots
If you don’t have these installed, run install.packages(pkg_names) with the package names as a character vector (pkg_names <- c("rvest", "quantmod", ...)). I also recommend the open-source RStudio IDE, which makes R Programming easy and efficient.
Russell 2K Analysis: Part 1
In part 1, the goal is to gain an overall understanding of the Russell 2000 Index. We’ll perform the following:
- Get the Russell 2K Stocks: Web Scraping with rvest
- Get Historical Prices and Log Returns: Function Mapping with quantmod and purrr
- Visualize the Relationship between Std Dev and Mean
- Develop a Screening Metric: Reward-to-Risk Metric
- Visually Screen with Plotly
Get the Russell 2K Stocks: Web Scraping with rvest
It turns out that it is rather difficult to find the list of Russell 2000 stocks. The best website I found was www.marketvolume.com. The list is spread across tables on nine HTML pages, each containing roughly 250 stock components. We’ll collect the components using the rvest package. To start, we get the base path and row numbers for each of the nine webpages.
# Base path and page rows from www.marketvolume.com
base_path <- "http://www.marketvolume.com/indexes_exchanges/r2000_components.asp?s=RUT&row="
row_num <- seq(from = 0, by = 250, length.out = 9)
Next, we create a function that we can map() using the purrr package. The function, get_stocklist(), takes the base_path and the row_num, and using rvest functions produces a table of stocks.
get_stocklist <- function(base_path, row_num) {
path <- paste0(base_path, row_num)
# rvest functions: Get table of stocks
stock_table <- read_html(path) %>%
html_node("table") %>%
html_table()
# Format table
stock_table <- stock_table[-1, 1:2] %>%
as_tibble() %>%
rename(symbol = X1, company = X2)
stock_table
}
As an example, we can apply get_stocklist() to the first page of nine, which is “row=0” in the html path.
get_stocklist(base_path, 0)
## # A tibble: 251 × 2
## symbol company
## * <chr> <chr>
## 1 FLWS 1-800 FLOWERS.COM
## 2 TWOU 2U, Inc.
## 3 DDD 3D SYSTEMS
## 4 EGHT 8X 8 INC
## 5 SHLM A SCHULMAN
## 6 ATEN A10 Networks, Inc.
## 7 AAC AAC Holdings, Inc.
## 8 AAON AAON
## 9 AIR AAR
## 10 AAN AARON'S
## # ... with 241 more rows
Finally, we create a data frame of row numbers using the row_num vector. Using the purrr::map() function, we iterate the get_stocklist() function across each of the row numbers. The result is a nested data frame with two levels. Using tidyr::unnest(), we get the full list of Russell 2000 stocks on one level. The rest of the pipe (%>%) operations after unnest() just tidy the data.
stocklist <- tibble(row_num) %>%
mutate(
stock_table = map(row_num,
function(.x) get_stocklist(base_path = base_path,
row_num = .x)
)
) %>%
unnest() %>%
select(-row_num) %>%
mutate_all(function(x) str_trim(x, side = 'both') %>% str_to_upper()) %>%
distinct()
The end result is a data frame of the Russell 2000 stocks:
stocklist
## # A tibble: 2,004 × 2
## symbol company
## <chr> <chr>
## 1 FLWS 1-800 FLOWERS.COM
## 2 TWOU 2U, INC.
## 3 DDD 3D SYSTEMS
## 4 EGHT 8X 8 INC
## 5 SHLM A SCHULMAN
## 6 ATEN A10 NETWORKS, INC.
## 7 AAC AAC HOLDINGS, INC.
## 8 AAON AAON
## 9 AIR AAR
## 10 AAN AARON'S
## # ... with 1,994 more rows
Get Historical Prices and Log Returns: Function Mapping with quantmod and purrr
Now that we have a list of the Russell 2000 stocks, we can collect some information. We need:
-
Historical Stock Prices: The daily stock prices are used to calculate the daily log returns. The function quantmod::getSymbols() returns the stock prices. We use a wrapper function, get_stock_prices(), to return the stock prices as a data frame in a consistent format needed for the unnesting() process.
-
Daily Log Returns: Log returns are the basis for quantitative stock analysis, which enables statistical prediction of future stock prices using the mean and standard deviation of the log returns. The mean drives the growth rate, and the standard deviation drives the stock volatility. The function quantmod::periodReturns() returns the logarithmic daily returns by setting period = "daily" and type = "log". We use a wrapper function, get_log_returns(), to return the log returns from the historical stock prices as a data frame in a consistent format needed for the mapping process.
The code for the wrapper functions are provided below:
# Wrapper for quantmod::getSymbols()
get_stock_prices <- function(ticker, return_format = "tibble", ...) {
# Get stock prices
stock_prices_xts <- getSymbols(Symbols = ticker, auto.assign = FALSE, ...)
# Rename
names(stock_prices_xts) <- c("Open", "High", "Low", "Close", "Volume", "Adjusted")
# Return in xts format if tibble is not specified
if (return_format == "tibble") {
stock_prices <- stock_prices_xts %>%
as_tibble() %>%
rownames_to_column(var = "Date") %>%
mutate(Date = ymd(Date))
} else {
stock_prices <- stock_prices_xts
}
stock_prices
}
# Wrapper for quantmod::periodReturns()
get_log_returns <- function(x, return_format = "tibble", period = 'daily', ...) {
# Convert tibble to xts
if (!is.xts(x)) {
x <- xts(x[,-1], order.by = x$Date)
}
# Get stock prices
log_returns_xts <- periodReturn(x = x$Adjusted, type = 'log', period = period, ...)
# Rename
names(log_returns_xts) <- "Log.Returns"
# Return in xts format if tibble is not specified
if (return_format == "tibble") {
log_returns <- log_returns_xts %>%
as_tibble() %>%
rownames_to_column(var = "Date") %>%
mutate(Date = ymd(Date))
} else {
log_returns <- log_returns_xts
}
log_returns
}
An example usage of get_stock_prices():
get_stock_prices("AAPL")
## # A tibble: 2,496 × 7
## Date Open High Low Close Volume Adjusted
## <date> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 2007-01-03 86.29 86.58 81.90 83.80 309579900 10.90416
## 2 2007-01-04 84.05 85.95 83.82 85.66 211815100 11.14619
## 3 2007-01-05 85.77 86.20 84.40 85.05 208685400 11.06681
## 4 2007-01-08 85.96 86.53 85.28 85.47 199276700 11.12147
## 5 2007-01-09 86.45 92.98 85.15 92.57 837324600 12.04533
## 6 2007-01-10 94.75 97.80 93.45 97.00 738220000 12.62176
## 7 2007-01-11 95.94 96.78 95.10 95.80 360063200 12.46562
## 8 2007-01-12 94.59 95.06 93.23 94.62 328172600 12.31207
## 9 2007-01-16 95.68 97.25 95.45 97.10 311019100 12.63477
## 10 2007-01-17 97.56 97.60 94.82 94.95 411565000 12.35501
## # ... with 2,486 more rows
And, an example usage of get_log_returns():
"AAPL" %>%
get_stock_prices() %>%
get_log_returns()
## # A tibble: 2,496 × 2
## Date Log.Returns
## <date> <dbl>
## 1 2007-01-03 0.000000000
## 2 2007-01-04 0.021952915
## 3 2007-01-05 -0.007146656
## 4 2007-01-08 0.004926215
## 5 2007-01-09 0.079799676
## 6 2007-01-10 0.046745766
## 7 2007-01-11 -0.012448172
## 8 2007-01-12 -0.012393888
## 9 2007-01-16 0.025872526
## 10 2007-01-17 -0.022390960
## # ... with 2,486 more rows
We can now get the mean() and sd() of the log returns. We can also get the number of trade days using the nrow() or length() functions.
funs <- c(mean.log.returns = mean, sd.log.returns = sd, n.trade.days = length)
aapl_log_returns <- "AAPL" %>%
get_stock_prices() %>%
get_log_returns()
sapply(funs, function(f) f(aapl_log_returns$Log.Returns))
## mean.log.returns sd.log.returns n.trade.days
## 9.312986e-04 2.085874e-02 2.496000e+03
As we’ll see in the next section, these features are important to the risk-reward trade-off. For now, we need to collect these values for the list of stocks. We do this using purrr::map() to apply functions to lists stored inside data frames. The next code chunk is the most complex of the post. Basically, we use the functions created previously to iteratively download the stock prices and compute the log returns. I added the proc.time() functions to time the code. It will take about 15 minutes to run.
Warning: The following script stores the stock prices and log returns for the entire list of 2000+ Russell 2000 stock components. It takes my laptop a about 15 minutes to run the script.
## user system elapsed
## 211.21 2.88 407.80
# Use purrr to map the functions across the entire list of Russell 2000 stocks
# Warning: This takes about 15 minutes
# Start the clock!
ptm <- proc.time()
from <- "2007-01-01"
to <- today()
stocklist <- stocklist %>%
mutate(
stock.prices = map(symbol,
function(.x) tryCatch({
get_stock_prices(.x,
return_format = "tibble",
from = from,
to = to)
}, error = function(e) {
NA
})
),
len = map_int(stock.prices, length)
) %>%
filter(len > 1) %>%
select(-len) %>%
mutate(
log.returns = map(stock.prices,
function(.x) get_log_returns(.x, return_format = "tibble")),
mean.log.returns = map_dbl(log.returns, ~ mean(.$Log.Returns)),
sd.log.returns = map_dbl(log.returns, ~ sd(.$Log.Returns)),
n.trade.days = map_dbl(stock.prices, nrow)
)
# Stop the clock
proc.time() - ptm
And, a peek at the contents of stocklist:
stocklist
## # A tibble: 1,187 × 7
## symbol company stock.prices
## <chr> <chr> <list>
## 1 FLWS 1-800 FLOWERS.COM <tibble [2,496 × 7]>
## 2 DDD 3D SYSTEMS <tibble [2,496 × 7]>
## 3 EGHT 8X 8 INC <tibble [2,496 × 7]>
## 4 SHLM A SCHULMAN <tibble [2,496 × 7]>
## 5 AAON AAON <tibble [2,496 × 7]>
## 6 AIR AAR <tibble [2,496 × 7]>
## 7 AAN AARON'S <tibble [2,496 × 7]>
## 8 ABAX ABAXIS <tibble [2,495 × 7]>
## 9 ANF ABERCROMBIE & FITCH <tibble [2,496 × 7]>
## 10 ABM ABM INDUSTRIES <tibble [2,496 × 7]>
## # ... with 1,177 more rows, and 4 more variables: log.returns <list>,
## # mean.log.returns <dbl>, sd.log.returns <dbl>, n.trade.days <dbl>
What is stocklist? It’s the historical stock prices and log returns for every stock in the Russell 2000 index. The stock prices and log returns are stored as nested lists inside the top-level data frame. We can access them like a list. Here’s the stock prices for the first observation in the list, 1-800 FLOWERS.COM, ticker symbol FLWS:
stocklist$stock.prices[[1]]
## # A tibble: 2,496 × 7
## Date Open High Low Close Volume Adjusted
## <date> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 2007-01-03 6.19 6.50 6.13 6.20 416500 6.20
## 2 2007-01-04 6.21 6.49 6.13 6.40 213300 6.40
## 3 2007-01-05 6.35 6.36 6.15 6.16 236500 6.16
## 4 2007-01-08 6.19 6.24 6.11 6.12 127100 6.12
## 5 2007-01-09 6.10 6.16 5.88 6.01 257900 6.01
## 6 2007-01-10 5.93 6.05 5.84 5.97 356700 5.97
## 7 2007-01-11 5.98 6.10 5.95 6.00 181000 6.00
## 8 2007-01-12 6.00 6.13 5.99 6.04 211000 6.04
## 9 2007-01-16 6.04 6.21 6.03 6.15 212100 6.15
## 10 2007-01-17 6.15 6.24 6.14 6.20 98000 6.20
## # ... with 2,486 more rows
Visualize the Relationship between Std Dev and Mean
Now that we have the mean daily log returns (MDLR) and the standard deviation of daily log returns (SDDLR), we can start to visualize the data. The next plot shows an important trend: the relationship between SDDLR and MDLR. We first filter out stocks with the number of trade days (n.trade.days) less than 2494 so each stock retained has the same large number of samples. Each year has approximately 250 trade days, so this filters out stocks with less than ten years of data to trend. Next, we limit stocks to those with SDDLR below 0.075. This allows us to zoom in on the vast majority of stocks. Plotting the trend using ggplot2 shows an interesting phenomenon: stocks with a high SDDLR tend to perform worse than those with a low SDDLR.
trade_day_thresh <- 2494
sd_limit <- 0.075
stocklist %>%
filter(n.trade.days >= trade_day_thresh,
sd.log.returns <= sd_limit) %>%
ggplot(aes(x = sd.log.returns, y = mean.log.returns)) +
geom_point(alpha = 0.1) +
geom_smooth() +
labs(title = "Market Tends to Penalize Stocks with Large SDDLR",
subtitle = "Best to Focus on Stocks with Highest Ratio of MDLR to SDDLR",
x = "Standard Deviation of Daily Log Returns (SDDLR)",
y = "Mean Daily Log Returns (MDLR)")
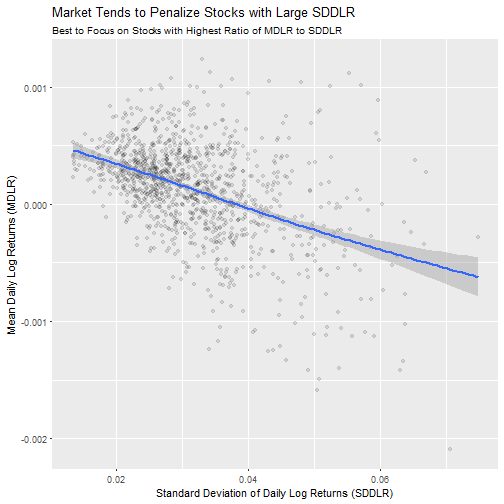
The important point is that, while volatile stocks may have one or two good years, over the long haul the less volatile stocks are where you want to put your money. We can develop a screening metric using this rationale.
Develop a Screening Metric: Reward-to-Risk Metric
The screening metric we will use is a reward-to-risk metric. We want to reward stocks with high MDLR (growth rate). We want to penalize stocks with high SDDLR (volatility), since these stocks tend to perform worse over time. The constant, 2500, is multiplied to yield values generally in the range of 100 to -100. The equation then becomes:
\[R = 2500*\frac{\mu}{\sigma}\]
Where,
- R is the reward-to-risk metric
- mu is the MDLR
- sigma is the SDDLR
Now we can add the reward-to-risk metric (reward.metric) to our data frame. We remove stocks with less than ten years of trading data, then add the reward-to-risk metric.
stocklist <- stocklist %>%
filter(n.trade.days >= 2494) %>%
mutate(reward.metric = 2500 * (mean.log.returns / sd.log.returns))
Visually Screen with Plotly
Let’s use the reward.metric to generate a visualization we can use for screening the stocks and understanding the index. Similar to the S&P500 post, we generate an interactive visualization using plotly. However, this time we use the reward.metric to drive the color and size of the markers, which enables us to visually see which stocks are scoring high on risk-to-reward. The best stocks have a green color, and the worse stocks have a brown color. We can pan, zoom, and hover over stocks to gain additional insights.
The code chunk to generate this visualization:
# Inputs
trade_day_thresh <- 2494
lab <- "Russell 2000"
back_col <- '#2C3E50'
font_col <- '#FFFFFF'
line_col <- "#FFFFFF"
grid_col <- 'rgb(255, 255, 255)'
col_brew_pal <- 'BrBG'
# Plotly
plot_ly(data = stocklist %>% filter(n.trade.days >= trade_day_thresh),
type = "scatter",
mode = "markers",
x = ~ sd.log.returns,
y = ~ mean.log.returns,
color = ~ reward.metric,
colors = col_brew_pal,
size = ~ reward.metric,
text = ~ str_c("<em>", company, "</em><br>",
"Ticker: ", symbol, "<br>",
"No. of Trading Days: ", n.trade.days, "<br>",
"Reward to Risk: ", round(reward.metric, 1)),
marker = list(opacity = 0.8,
symbol = 'circle',
sizemode = 'diameter',
sizeref = 4.0,
line = list(width = 2, color = line_col))
) %>%
layout(title = str_c(lab, 'Analysis: Stock Risk vs Reward', sep = " "),
xaxis = list(title = 'Risk: StDev of Daily Log Returns (SDDLR)',
gridcolor = grid_col,
zerolinewidth = 1,
ticklen = 5,
gridwidth = 2),
yaxis = list(title = 'Reward: Mean Daily Log Returns (MDLR)',
gridcolor = grid_col,
zerolinewidth = 1,
ticklen = 5,
gridwith = 2),
margin = list(l = 100,
t = 100,
b = 100),
font = list(color = font_col),
paper_bgcolor = back_col,
plot_bgcolor = back_col)
Russell 2K Analysis: Part 2
The end goal is to find the best stocks, and we don’t want to simply trust the reward-to-risk metric. Rather, we want to review the characteristics of the top stocks so we can select those with the most consistent growth. In this section, we perform the following:
Visualize Top 15 Stocks to Understand Consistent Growth
We begin by filtering the stocklist, first ranking by the reward.metric then selecting the top 15.
# Filter high performing stocks
top_n_limit <- 15
hp <- stocklist %>%
mutate(rank = reward.metric %>% desc() %>% min_rank()) %>%
filter(rank <= top_n_limit) %>%
arrange(rank)
hp %>%
select(symbol, rank, reward.metric)
## # A tibble: 15 × 3
## symbol rank reward.metric
## <chr> <int> <dbl>
## 1 MMS 1 108.96364
## 2 PLUS 2 102.11645
## 3 NEOG 3 102.02423
## 4 VGR 4 96.72998
## 5 CMN 5 96.72072
## 6 LANC 6 96.25926
## 7 CALM 7 95.06285
## 8 BOFI 8 94.05493
## 9 HIFS 9 93.84694
## 10 EBIX 10 93.51365
## 11 NATH 11 93.32580
## 12 AGX 12 91.46460
## 13 ATRI 13 91.26833
## 14 EXPO 14 90.82085
## 15 MGEE 15 90.62637
Next, we create a means_by_year() function to take a data frame of log.returns and return a data frame of MDLRs by year. We then map() the means_by_year() function to iterate over the full data frame of log returns.
# Function to return MDLR by year
means_by_year <- function(log.returns) {
log.returns %>%
mutate(year = year(Date)) %>%
group_by(year) %>%
summarize(mean.log.returns = mean(Log.Returns))
}
# Map function to data frame
hp <- hp %>%
mutate(means.by.year = map(log.returns, means_by_year))
# View resutls
hp %>% select(symbol, means.by.year)
## # A tibble: 15 × 2
## symbol means.by.year
## <chr> <list>
## 1 MMS <tibble [10 × 2]>
## 2 PLUS <tibble [10 × 2]>
## 3 NEOG <tibble [10 × 2]>
## 4 VGR <tibble [10 × 2]>
## 5 CMN <tibble [10 × 2]>
## 6 LANC <tibble [10 × 2]>
## 7 CALM <tibble [10 × 2]>
## 8 BOFI <tibble [10 × 2]>
## 9 HIFS <tibble [10 × 2]>
## 10 EBIX <tibble [10 × 2]>
## 11 NATH <tibble [10 × 2]>
## 12 AGX <tibble [10 × 2]>
## 13 ATRI <tibble [10 × 2]>
## 14 EXPO <tibble [10 × 2]>
## 15 MGEE <tibble [10 × 2]>
Then, we unnest() the high performers to get a one-level data frame. Voila, we have mean.log.returns by year for each stock.
# Unnest high performing stocks
hp_unnest <- hp %>%
select(symbol, means.by.year) %>%
unnest()
hp_unnest
## # A tibble: 150 × 3
## symbol year mean.log.returns
## <chr> <dbl> <dbl>
## 1 MMS 2007 1.016679e-03
## 2 MMS 2008 -3.295602e-04
## 3 MMS 2009 1.448253e-03
## 4 MMS 2010 1.108940e-03
## 5 MMS 2011 9.544601e-04
## 6 MMS 2012 1.726920e-03
## 7 MMS 2013 1.329424e-03
## 8 MMS 2014 8.907859e-04
## 9 MMS 2015 1.121939e-04
## 10 MMS 2016 1.189651e-05
## # ... with 140 more rows
Finally, we can visualize the results in ggplot2 using a facet plot.
# Visualize using ggplot
hp_unnest %>%
ggplot(aes(x = year, y = mean.log.returns)) +
geom_ref_line(h = 0) +
geom_line(aes(col = symbol)) +
geom_smooth(method = "lm", se = FALSE) +
facet_wrap(~ symbol, nrow = 3) +
theme(legend.position = "None", axis.text.x = element_text(angle=90)) +
labs(title = "Best Prospects Have Consistent, Above-Zero MDLR and Growth",
subtitle = "Trend Flat to Upward Indicates Growth",
x = "Year",
y = "Mean Daily Log Returns (MDLR)")
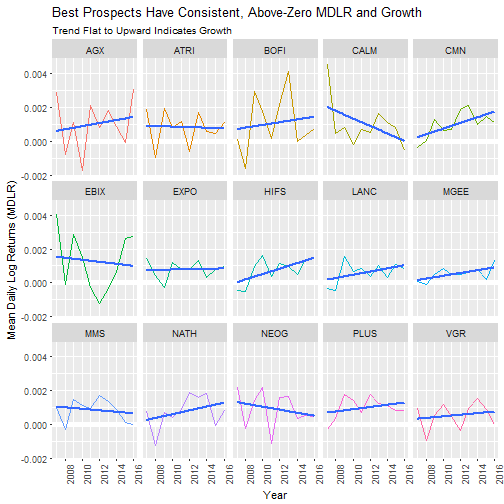
When reviewing the facet plot, we want to select stocks with the following attributes that the market tends to reward:
-
Above zero MDLR: Every time a stocks MDLR drops below zero, the stock loses money for that year. All of the stocks drop below zero at least once. Those that drop below zero multiple times become bad investments in those respective years. We want good investments over the long haul, or in other words stocks with consistent, above-zero MDLR.
-
Flat or Upward Growth Trends: Remember, we are viewing MDLR, which is the growth rate. A flat trend means the stock is consistently growing. An upward trend means the stock’s growth rate is accelerating. A downward trend means the stocks growth rate is slowing. We want flat or upward growth.
-
Low Standard Deviation of MDLR by Year: Again, the market loves consistency. Less volatility makes for a more profitable investment.
We have two options now:
- We can manually review each chart to decide which stocks we want to invest in, or
- We can develop a method to programmatically rank the stocks.
Always opt for programmatic review! Programmatic review is less prone to errors and can be applied to a much larger set of stocks (ergo, while 15 stocks may be easy, 1500 becomes very difficult).
For the programatic review, we need to compute the three desired attributes of high performing stocks:
- The number of times the stock’s MDLR by year drops below zero (bad)
- The slope of the trend line of MDLR by year ()
- The standard deviation of MDLR by year
Attribute 1: Number of Times MDLR by Year Drops Below Zero
First, the number of times the stock drops below zero. We create a function means_below_zero() that takes a data frame of means.by.year for one stock and returns the number of MDLRs by year that are less than zero. We then map the function using map_dbl(). Note that we use the map_dbl() version of map() because map() returns a list and map_dbl() returns a number. We want a number, not a list with the number in it.
# Function to return number of times a stock's MDLR by year drops below zero
means_below_zero <- function(means.by.year) {
means.by.year %>%
filter(mean.log.returns < 0) %>%
nrow()
}
# Map function to data frame for all stocks
hp <- hp %>%
mutate(means.below.zero = map_dbl(means.by.year, means_below_zero))
# View the results
hp %>% select(symbol, means.below.zero)
## # A tibble: 15 × 2
## symbol means.below.zero
## <chr> <dbl>
## 1 MMS 1
## 2 PLUS 1
## 3 NEOG 2
## 4 VGR 2
## 5 CMN 1
## 6 LANC 2
## 7 CALM 2
## 8 BOFI 2
## 9 HIFS 2
## 10 EBIX 4
## 11 NATH 2
## 12 AGX 3
## 13 ATRI 2
## 14 EXPO 1
## 15 MGEE 1
Attribute 2: Slope of MDLR by Year
Next, we need to get the slope of the linear trend. The method we use is slightly more complex because we need to get the second coefficient of the linear model, but it is extremely powerful because we are applying models to data frames. We’ll follow the process outlined in R for Data Science, Chapter 25: Many Models.
We create a means_by_year_model() function to apply a linear model to a single stock. The function takes a data frame of means.by.year for the stock, and returns the model from the lm() function.
means_by_year_model <- function(means.by.year) {
lm(mean.log.returns ~ year, data = means.by.year)
}
Let’s test it out on the first stock, MAXIMUS, ticker symbol MMS:
hp$means.by.year[[1]] %>%
means_by_year_model()
##
## Call:
## lm(formula = mean.log.returns ~ year, data = means.by.year)
##
## Coefficients:
## (Intercept) year
## 8.987e-02 -4.427e-05
We are interested in the coefficient for year, so let’s make one more function to extract the slope coefficient.
slope <- function(means.by.year.model) {
means.by.year.model$coefficients[[2]]
}
Again, let’s test it out on MMS to validate the workflow:
hp$means.by.year[[1]] %>%
means_by_year_model() %>%
slope()
## [1] -4.426781e-05
Now we are ready to apply the modeling and slope functions to the data frame:
# Map modeling and slope functions
hp <- hp %>%
mutate(
means.by.year.model = map(means.by.year, means_by_year_model),
slope = map_dbl(means.by.year.model, slope)
)
# View the results
hp %>% select(symbol, means.by.year.model, slope)
## # A tibble: 15 × 3
## symbol means.by.year.model slope
## <chr> <list> <dbl>
## 1 MMS <S3: lm> -4.426781e-05
## 2 PLUS <S3: lm> 6.553556e-05
## 3 NEOG <S3: lm> -8.914962e-05
## 4 VGR <S3: lm> 4.692651e-05
## 5 CMN <S3: lm> 1.687568e-04
## 6 LANC <S3: lm> 9.490521e-05
## 7 CALM <S3: lm> -2.212729e-04
## 8 BOFI <S3: lm> 8.023846e-05
## 9 HIFS <S3: lm> 1.604588e-04
## 10 EBIX <S3: lm> -6.009229e-05
## 11 NATH <S3: lm> 1.133269e-04
## 12 AGX <S3: lm> 9.195434e-05
## 13 ATRI <S3: lm> -1.634960e-05
## 14 EXPO <S3: lm> 1.080354e-05
## 15 MGEE <S3: lm> 8.274274e-05
Great! We now have the linear models and the slope of the linear trend line.
Attribute 3: Standard deviation of MDLR by year
Finally, to drive home consistency, we need the standard deviation of the MDLR by year. To do this we create a sd_of_means_by_year() function that simply computes the sd() of the MDLR by year. The function is then mapped the data frame using map_dbl(), which returns the numeric value.
# Function to return sd() of mean log returns by year
sd_of_means_by_year <- function(means.by.year) {
sd(means.by.year$mean.log.returns)
}
# Map to data frame
hp <- hp %>%
mutate(sd.of.means.by.year = map_dbl(means.by.year, sd_of_means_by_year))
# View results
hp %>% select(symbol, sd.of.means.by.year)
## # A tibble: 15 × 2
## symbol sd.of.means.by.year
## <chr> <dbl>
## 1 MMS 0.0006747014
## 2 PLUS 0.0006521073
## 3 NEOG 0.0010957728
## 4 VGR 0.0007623495
## 5 CMN 0.0007775752
## 6 LANC 0.0006314911
## 7 CALM 0.0013962898
## 8 BOFI 0.0016739914
## 9 HIFS 0.0007489171
## 10 EBIX 0.0017504762
## 11 NATH 0.0009466021
## 12 AGX 0.0015549293
## 13 ATRI 0.0009788187
## 14 EXPO 0.0005275523
## 15 MGEE 0.0004111271
Develop a Ranking Metric: Growth-to-Consistency
To assist in the final ranking process we’ll use a growth-to-consistency ranking metric, one that incorporates the means.below.zero, slope of the linear trend line, and sd.of.means.by.year for MDLR by year. We develop the following measure that rewards stocks with positive growth rate and that penalizes stocks with high volatility year-to-year and multiple years of negative returns.
\[G = \frac{m}{(n + 1)*s}\]
Where,
- m is the slope of the linear trend line
- n is the number of times the MDLR goes below zero
- s is the standard deviation of the MDLR by year
Now we add the new, growth-to-consistency metric (growth.metric) to our data frame, and view the results.
hp <- hp %>%
mutate(growth.metric = slope /((means.below.zero + 1) * sd.of.means.by.year))
hp %>% select(symbol, growth.metric, slope, means.below.zero, sd.of.means.by.year) %>%
arrange(desc(growth.metric)) %>%
knitr::kable() # Nice table format
| symbol |
growth.metric |
slope |
means.below.zero |
sd.of.means.by.year |
| CMN |
0.1085148 |
0.0001688 |
1 |
0.0007776 |
| MGEE |
0.1006291 |
0.0000827 |
1 |
0.0004111 |
| HIFS |
0.0714181 |
0.0001605 |
2 |
0.0007489 |
| PLUS |
0.0502491 |
0.0000655 |
1 |
0.0006521 |
| LANC |
0.0500958 |
0.0000949 |
2 |
0.0006315 |
| NATH |
0.0399066 |
0.0001133 |
2 |
0.0009466 |
| VGR |
0.0205184 |
0.0000469 |
2 |
0.0007623 |
| BOFI |
0.0159775 |
0.0000802 |
2 |
0.0016740 |
| AGX |
0.0147843 |
0.0000920 |
3 |
0.0015549 |
| EXPO |
0.0102393 |
0.0000108 |
1 |
0.0005276 |
| ATRI |
-0.0055678 |
-0.0000163 |
2 |
0.0009788 |
| EBIX |
-0.0068658 |
-0.0000601 |
4 |
0.0017505 |
| NEOG |
-0.0271193 |
-0.0000891 |
2 |
0.0010958 |
| MMS |
-0.0328055 |
-0.0000443 |
1 |
0.0006747 |
| CALM |
-0.0528240 |
-0.0002213 |
2 |
0.0013963 |
Finally, we are ready to visualize the performance of the top six stocks. The code chunk below ranks high performance stocks by the growth-to-consistency metric (growth.metric), then filters to the top six. From that point, the symbol and stock.prices are selected and unnested to return the historical stock prices for each symbol in the top six performers. Last, a facet plot is made using the historical stock prices adjusted for stock splits. These are the top performers!
top_n_limit <- 6
hp %>%
mutate(rank = growth.metric %>% desc() %>% min_rank()) %>%
filter(rank <= top_n_limit) %>%
select(symbol, stock.prices) %>%
unnest() %>%
ggplot(aes(x = Date, y = Adjusted, col = symbol)) +
geom_line() +
facet_wrap(~ symbol, nrow = 3, scales = "free_y") +
theme(legend.position = "None") +
labs(title = "Prospecting Best Russell 2000 Stocks",
subtitle = "Six Small Caps with Amazing Growth, Most Consistency",
x = "Year",
y = "Price per Share")

Questions About the Analysis
-
Should you simply invest in the stocks screened? Why or why not? (Hint: What else about the stocks and/or companies should you investigate?)
-
Are there other factors not considered in the metrics that should be included? (Hint: What do characteristics do some of the top 15 performers have that is not included in the final metric, G?)
-
Can you combine the two metrics, R and G, into one metric that can be computed for the entire data frame of all Russell 2000 stocks?
Download the .R File
The full code for the tutorial can be downloaded as a .R file here. The code will take approximately 15 minutes to run.
Conclusion
As shown in the previous S&P500 Analysis Post, quantitative analysis is a powerful tool. By applying data science techniques using R programming and the various packages (e.g. tidyverse, quantmod, purrr, etc), we can evaluate massive data sets and quickly screen the stocks using reward-to-risk and growth-to-consistency metrics. However, a word of caution before jumping into any investments: Selecting investments on statistical analysis alone is never a good idea. The statistical analysis allows us to screen stocks as potential investments, but a thorough analysis of the company and the stock should be performed. Evaluation of stock and company fundamentals such as asset valuation (forward and trailing P/E ratio), industry analysis, diversification, etc should be pursued prior to making any investment decision. With that said, the screening process described herein is an excellent first step. Once you have investments worth investigating, I recommend reading articles on a website such as Seeking Alpha from experts with experience covering the stocks of interest.
Recap
Well done if you made it this far! This post covered a vast array of R programming functions, data management workflows, and data science techniques that can be used regardless of the application. The Russell 2000 Post extended the investment screening analysis from the previous S&P500 Analysis Post by using a variety of data science and modeling techniques.
To summarize:
-
We built custom functions to retrieve stock symbols, historical stock prices, and daily log returns. We used a custom function to web scrape stock symbols, leveraging the rvest package. We also used custom functions as wrappers for getSymbols() and periodReturns() functions from the quantmod library. We mapped the custom functions to data frames using the purrr::map() function. The result was a data frame of stock prices and daily log returns for every stock in the Russell 2000 index.
-
We visualized the relationship between MDLR and SDDLR using ggplot2, which gave us insight into how stocks function within the market. We used this information to develop a reward-to-risk metric that served as a useful way to screen stocks when applied to an interactive screening visualization using plotly.
-
We pared down the list to the top 15 stocks, manipulating the data to visualize the level of consistency of our high performers using ggplot2. We then developed three desirable attributes of high performers. The attributes were added using the data modeling workflow, which consists of creating functions that return data frames, lists, or values and mapping the functions using purrr.
-
We developed a final metric that measured growth-to-consistency of our high performers. This measure enabled us to rank the high performers, and select the top 6 for further review. The share price performance of the top 6 was visualized using ggplot2.
Great work! If you understand this post, you now have many tools at your disposal that apply to much more than just investment analysis.
Further Reading
-
R For Data Science, Chapter 25: Many Models: Chapter 25 covers the workflow for modeling many models using tidyverse, purrr, and modelr packages. This a very powerful resource that helps you extend a single model to many models. The entire R for Data Science book is free and online.
-
Seeking Alpha: A website for the investing community focused on providing investment analysis and insight. Once you have screened stocks, a next logical step is to collect information. The analysis provided on SA can help you finalize your investment decisions.